Electron. J. Differential Equations,
Vol. 2017 (2017), No. 180, pp. 1-15.
Sign-changing solutions for non-local elliptic equations
Huxiao Luo
Abstract:
This article concerns the existence of sign-changing solutions for equations
driven by a non-local integrodifferential operator with homogeneous
Dirichlet boundary conditions,
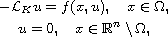
where
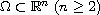 is a bounded, smooth domain and
the nonlinear term f satisfies suitable growth assumptions.
By using Brouwer's degree theory and Deformation Lemma and arguing as
in [2], we prove that there exists a least energy sign-changing
solution. Our results generalize and improve some results obtained in [27]
is a bounded, smooth domain and
the nonlinear term f satisfies suitable growth assumptions.
By using Brouwer's degree theory and Deformation Lemma and arguing as
in [2], we prove that there exists a least energy sign-changing
solution. Our results generalize and improve some results obtained in [27]
Submitted March 30, 2017. Published July 14, 2017.
Math Subject Classifications: 35R11, 58E30.
Key Words: Brouwer's degree theory; sign-changing solutions;
non-local elliptic equations; deformation Lemma.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Huxiao Luo
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: luohuxiao1989@163.com
|
|---|
Return to the EJDE web page
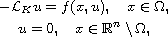
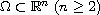 is a bounded, smooth domain and
the nonlinear term f satisfies suitable growth assumptions.
By using Brouwer's degree theory and Deformation Lemma and arguing as
in [2], we prove that there exists a least energy sign-changing
solution. Our results generalize and improve some results obtained in [27]
is a bounded, smooth domain and
the nonlinear term f satisfies suitable growth assumptions.
By using Brouwer's degree theory and Deformation Lemma and arguing as
in [2], we prove that there exists a least energy sign-changing
solution. Our results generalize and improve some results obtained in [27]
