Electron. J. Differential Equations,
Vol. 2017 (2017), No. 183, pp. 1-28.
Multiplicity results of fractional-Laplace system with sign-changing
and singular nonlinearity
Sarika Goyal
Abstract:
In this article, we study the following fractional-Laplacian system
with singular nonlinearity
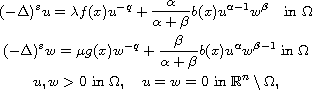
where
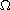 is a bounded domain in
is a bounded domain in
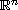 with smooth
boundary
with smooth
boundary
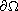 ,
,
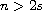 ,
,
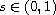 ,
,
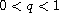 ,
,
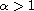 ,
,
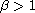 satisfy
satisfy
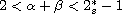 with
with
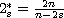 , the pair
of parameters
, the pair
of parameters
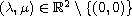 .
The weight functions
.
The weight functions
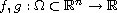 such
that
such
that
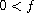 ,
,
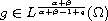 ,
and
,
and
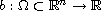 is a sign-changing function such
that
is a sign-changing function such
that
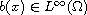 .
Using variational methods, we show existence
and multiplicity of positive solutions with respect to the
pair of parameters
.
Using variational methods, we show existence
and multiplicity of positive solutions with respect to the
pair of parameters
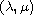 .
.
Submitted July 20, 2016. Published July 18, 2017.
Math Subject Classifications: 35A15, 35J75, 35R11.
Key Words: Fractional-Laplacian system; singular nonlinearity;
sign-changing weight function.
Show me the PDF file (335 KB),
TEX file for this article.
 |
Sarika Goyal
Department of Mathematics
Bennett University, Greater Noida
Uttar Pradesh, India
email: sarika1.iitd@gmail.com, sarika.goyal@bennett.edu.in
|
|---|
Return to the EJDE web page
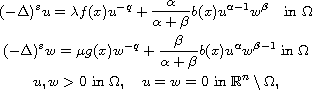
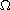 is a bounded domain in
is a bounded domain in
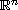 with smooth
boundary
with smooth
boundary
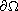 ,
,
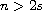 ,
,
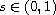 ,
,
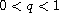 ,
,
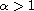 ,
,
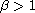 satisfy
satisfy
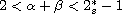 with
with
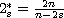 , the pair
of parameters
, the pair
of parameters
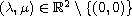 .
The weight functions
.
The weight functions
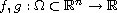 such
that
such
that
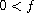 ,
,
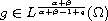 ,
and
,
and
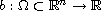 is a sign-changing function such
that
is a sign-changing function such
that
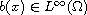 .
Using variational methods, we show existence
and multiplicity of positive solutions with respect to the
pair of parameters
.
Using variational methods, we show existence
and multiplicity of positive solutions with respect to the
pair of parameters
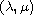 .
.
