Electron. J. Differential Equations,
Vol. 2017 (2017), No. 208, pp. 1-14.
Existence of infinitely many solutions for fractional p-Laplacian equations
with sign-changing potential
Youpei Zhang, Xianhua Tang, Jian Zhang
Abstract:
In this article, we prove the existence of infinitely many solutions
for the fractional
 -Laplacian equation
-Laplacian equation
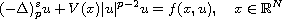
where
 ,
,
 .
Based on a direct sum decomposition
of a space
.
Based on a direct sum decomposition
of a space
 ,
we investigate the multiplicity of solutions
for the fractional p-Laplacian equation in
,
we investigate the multiplicity of solutions
for the fractional p-Laplacian equation in
 .
The potential
V is allowed to be sign-changing, and the primitive of the nonlinearity
f is of super-p growth near infinity in u and allowed to be sign-changing.
Our assumptions are suitable and different from those studied previously.
.
The potential
V is allowed to be sign-changing, and the primitive of the nonlinearity
f is of super-p growth near infinity in u and allowed to be sign-changing.
Our assumptions are suitable and different from those studied previously.
Submitted January 25, 2017. Published September 8, 2017.
Math Subject Classifications: 35J60, 35J20.
Key Words: Fractional p-Laplacian; multiple solutions; variational methods;
sign-changing potential.
Show me the PDF file (290 KB),
TEX file for this article.
 |
Youpei Zhang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: zhangypzn@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Jian Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page
 -Laplacian equation
-Laplacian equation
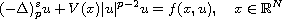
 ,
,
 .
Based on a direct sum decomposition
of a space
.
Based on a direct sum decomposition
of a space
 ,
we investigate the multiplicity of solutions
for the fractional p-Laplacian equation in
,
we investigate the multiplicity of solutions
for the fractional p-Laplacian equation in
 .
The potential
V is allowed to be sign-changing, and the primitive of the nonlinearity
f is of super-p growth near infinity in u and allowed to be sign-changing.
Our assumptions are suitable and different from those studied previously.
.
The potential
V is allowed to be sign-changing, and the primitive of the nonlinearity
f is of super-p growth near infinity in u and allowed to be sign-changing.
Our assumptions are suitable and different from those studied previously.


