We study the existence of non-trivial weak solutions in
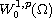 of the super-linear Dirichlet problem
of the super-linear Dirichlet problem
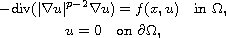
where f satisfies the condition
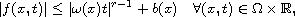
where
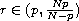 ,
,
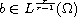 and
and
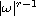 may be non-integrable on
may be non-integrable on
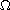 .
.
Duong Minh Duc
Abstract:
We study the existence of non-trivial weak solutions in
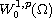 of the super-linear Dirichlet problem
of the super-linear Dirichlet problem
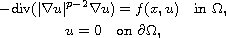
where f satisfies the condition
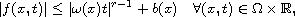
where
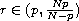 ,
,
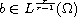 and
and
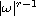 may be non-integrable on
may be non-integrable on
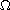 .
.
Submitted May 8, 2017. Published October 10, 2017.
Math Subject Classifications: 46E35, 35J20.
Key Words: Nemytskii operators; p-Laplacian; multiplicity of solutions;
mountain-pass theorem.
Show me the PDF file (247 KB), TEX file for this article.
 |
Duong Minh Duc University of Sciences Vietnam National University 227 Nguyen Van Cu Q5 Hochiminh City, Vietnam email: dmduc@hcmus.edu.vn |
|---|
Return to the EJDE web page