Electron. J. Differential Equations,
Vol. 2017 (2017), No. 267, pp. 1-15.
A priori error estimates of finite volume methods for general
elliptic optimal control problems
Yuming Feng, Zuliang Lu, Longzhou Cao, Lin Li, Shuhua Zhang
Abstract:
In this article, we establish a priori error estimates for the finite
volume approximation of general elliptic optimal control problems.
We use finite volume methods to discretize the state and adjoint
equation of the optimal control problems. For the variational
inequality, we use the variational discretization methods to
discretize the control. We show the existence and the uniqueness of
the solution for discrete optimality conditions. Under some
reasonable assumptions, we obtain some optimal order error estimates
for the state, costate and control variables. On one hand, the
convergence rate for the state, costate and control variables is
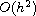 or
or
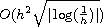 in the sense of
in the sense of
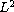 norm or
norm or
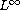 norm. On the other hand, the convergence rate
for the state and costate variables is
norm. On the other hand, the convergence rate
for the state and costate variables is
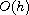 or
or
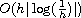 in the sense of
in the sense of
 norm or
norm or
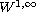 norm.
norm.
Submitted August 9, 2017. Published October 27, 2017.
Math Subject Classifications: 49J20, 65N30.
Key Words: A priori error estimates; general elliptic optimal control problems;
finite volume methods; optimal-order.
Show me the PDF file (301 KB),
TEX file for this article.
 |
Yuming Feng
Key Laboratory of Intelligent Information Processing and Control
Chongqing Three Gorges University
Wanzhou, Chongqing, 404100, China
email: yumingfeng25928@163.com
|
|---|
 |
Zuliang Lu
Key Laboratory for Nonlinear Science and System Structure
Chongqing Three Gorges University,
Chongqing 404100, China
email: zulianglux@126.com
|
|---|
 |
Longzhou Cao
Key Laboratory for Nonlinear Science and System Structure
Chongqing Three Gorges University
Chongqing 404100, China
email: caolongzhou@126.com
|
|---|
 |
Lin Li
Key Laboratory for Nonlinear Science and System Structure
Chongqing Three Gorges University
Chongqing 404100, China
email: linligx@126.com
|
|---|
 |
Shuhua Zhang
Research Center for Mathematics and Economics
Tianjin University of Finance and Economics
Tianjin 300222, China
email: szhang@tjufe.edu.cn
|
|---|
Return to the EJDE web page
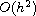 or
or
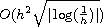 in the sense of
in the sense of
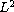 norm or
norm or
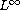 norm. On the other hand, the convergence rate
for the state and costate variables is
norm. On the other hand, the convergence rate
for the state and costate variables is
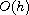 or
or
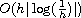 in the sense of
in the sense of
 norm or
norm or
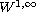 norm.
norm.




