Electron. J. Differential Equations, Vol. 2017 (2017), No. 27, pp. 1-18.

Multiple solutions of a fourth-order nonhomogeneous equation with critical growth in $\mathbb{R}^4$

Abhishek Sarkar

Abstract:
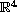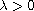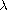In this article we study the existence of at least two positive weak solutions of an nonhomogeneous fourth-order Navier boundary-value problem involving critical exponential growth on a bounded domain in $\mathbb{R}^4$, with a parameter $\lambda >0$. We establish upper and lower bounds for $\lambda$, which determine multiplicity and non-existence of solutions.

Submitted September 12, 2016. Published January 24, 2017.
Math Subject Classifications: 35J30, 35J40, 35J60.
Key Words: Biharmonic; critical exponent; multiple solutions.

Show me the PDF file (297 KB), TEX file for this article.

Abhishek Sarkar
NTIS, University of West Bohemia
Technicka 8, 306 14 Plzen
Czech Republic
email: sarkara@ntis.zcu.cz

Return to the EJDE web page