In this article, we prove the existence and multiplicity of nontrivial solutions for the nonperiodic perturbed fractional Hamiltonian systems

where
![$\alpha \in (1/2 , 1],\; \lambda> 0 $](gifs/ab.gif) is a parameter,
is a parameter,
 ,
,
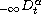 and
and
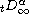 are left and right Liouville-Weyl fractional
derivatives of order
are left and right Liouville-Weyl fractional
derivatives of order
 on the whole axis
on the whole axis
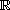 respectively,
the matrix
respectively,
the matrix
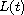 is not necessary positive definite for all
is not necessary positive definite for all
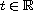 nor coercive,
nor coercive,
 and
and
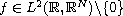 small enough.
Replacing the Ambrosetti-Rabinowitz Condition by general superquadratic
assumpt ions, we establish the existence and multiplicity results for the
above system. Some examples are also given to illustrate our results.
small enough.
Replacing the Ambrosetti-Rabinowitz Condition by general superquadratic
assumpt ions, we establish the existence and multiplicity results for the
above system. Some examples are also given to illustrate our results.
