Electron. J. Differential Equations,
Vol. 2018 (2018), No. 05, pp. 1-12.
Fractional Schrodinger equations with new conditions
Abderrazek Benhassine
Abstract:
In this article, we study the nonlinear fractional Schrodinger equation
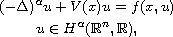
where
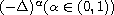 stands for the
fractional Laplacian of order
stands for the
fractional Laplacian of order
 ,
,
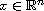 ,
,
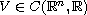 may change sign and f is
only locally defined near the origin with respect to u.
Under some new assumptions on V and f, we show that the above system
has infinitely many solutions near the origin. Some examples are also
given to illustrate our main theoretical result.
may change sign and f is
only locally defined near the origin with respect to u.
Under some new assumptions on V and f, we show that the above system
has infinitely many solutions near the origin. Some examples are also
given to illustrate our main theoretical result.
Submitted July 28, 2017. Published January 4, 2018.
Math Subject Classifications: 35B38, 35G99.
Key Words: Fractional Schrodinger equations; critical point theory;
symmetric mountain pass theorem.
Show me the PDF file (247 KB),
TEX file for this article.
 |
Abderrazek Benhassine
Department of Mathematics
Higher Institut for Informatics and Mathematics
5000, Monastir, Tunisia
email: ab.hassine@yahoo.com
|
|---|
Return to the EJDE web page
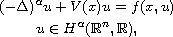
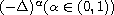 stands for the
fractional Laplacian of order
stands for the
fractional Laplacian of order
 ,
,
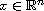 ,
,
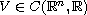 may change sign and f is
only locally defined near the origin with respect to u.
Under some new assumptions on V and f, we show that the above system
has infinitely many solutions near the origin. Some examples are also
given to illustrate our main theoretical result.
may change sign and f is
only locally defined near the origin with respect to u.
Under some new assumptions on V and f, we show that the above system
has infinitely many solutions near the origin. Some examples are also
given to illustrate our main theoretical result.
