Electron. J. Differential Equations,
Vol. 2018 (2018), No. 124, pp. 1-21.
Two solutions for nonhomogeneous Klein-Gordon-Maxwell system with
sign-changing potential
Lixia Wang, Shangjie Chen
Abstract:
In this article, we study the nonhomogeneous Klein-Gordon-Maxwell system
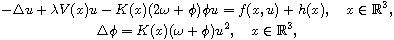
where
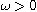 is a constant and
is a constant and
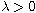 is a parameter.
Using the Linking theorem and Ekeland's variational principle
in critical point theory, we prove the existence of multiple solutions,
under suitable assumptions that allow a sign-changing potential.
is a parameter.
Using the Linking theorem and Ekeland's variational principle
in critical point theory, we prove the existence of multiple solutions,
under suitable assumptions that allow a sign-changing potential.
Submitted November 16, 2017. Published June 16, 2018.
Math Subject Classifications: 35B33, 35J65, 35Q55.
Key Words: Klein-Gordon-Maxwell system; mountain pass theorem;
nonhomogeneous; Ekeland's variational principle.
Show me the PDF file (327 KB),
TEX file for this article.
 |
Lixia Wang
School of Sciences
Tianjin Chengjian University
Tianjin 300384, China
email: wanglixia0311@126.com}
|
|---|
 |
Shangjie Chen
School of Mathematics and Statistics
Chongqing Technology and Business University
Chongqing 400067, China
email: chensj@ctbu.edu.cn
|
|---|
Return to the EJDE web page
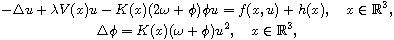
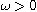 is a constant and
is a constant and
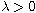 is a parameter.
Using the Linking theorem and Ekeland's variational principle
in critical point theory, we prove the existence of multiple solutions,
under suitable assumptions that allow a sign-changing potential.
is a parameter.
Using the Linking theorem and Ekeland's variational principle
in critical point theory, we prove the existence of multiple solutions,
under suitable assumptions that allow a sign-changing potential.

