Electron. J. Differential Equations,
Vol. 2018 (2018), No. 126, pp. 1-21.
Multiplicity of solutions for a perturbed fractional Schrodinger equation
involving oscillatory terms
Chao Ji, Fei Fang
Abstract:
In this article we study the perturbed fractional Schrodinger equation
involving oscillatory terms
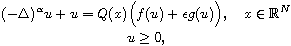
where
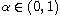 and
and
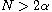 ,
,
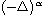 stands for
the fractional Laplacian,
stands for
the fractional Laplacian,
 is a radial,
positive potential,
is a radial,
positive potential,
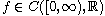 oscillates near the
origin or at infinity and
oscillates near the
origin or at infinity and
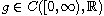 with
with
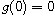 .
By using the variational method and the principle of symmetric criticality
for non-smooth Szulkin-type functionals, we establish that:
(1) the unperturbed problem, i.e. with
.
By using the variational method and the principle of symmetric criticality
for non-smooth Szulkin-type functionals, we establish that:
(1) the unperturbed problem, i.e. with
 has infinitely many
solutions;
(2) the number of distinct solutions becomes greater and greater when
has infinitely many
solutions;
(2) the number of distinct solutions becomes greater and greater when
 is smaller and smaller. Moreover, various properties of the
solutions are also described in terms of the
is smaller and smaller. Moreover, various properties of the
solutions are also described in terms of the
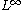 -
and
-
and
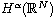 -norms.
-norms.
Submitted January 7, 2018. Published June 18, 2018.
Math Subject Classifications: 35J60, 47J30.
Key Words: Fractional Schrodinger equation; multiple solutions;
oscillatory terms.
Show me the PDF file (325 KB),
TEX file for this article.
 |
Chao Ji
Department of Mathematics
East China University of Science and Technology
200237 Shanghai, China
email: jichao@ecust.edu.cn
|
|---|
 |
Fei Fang
Department of Mathematics
Beijing Technology and Business University
100048 Beijing, China
email: fangfei68@163.com
|
|---|
Return to the EJDE web page
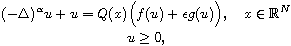
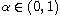 and
and
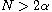 ,
,
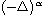 stands for
the fractional Laplacian,
stands for
the fractional Laplacian,
 is a radial,
positive potential,
is a radial,
positive potential,
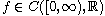 oscillates near the
origin or at infinity and
oscillates near the
origin or at infinity and
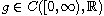 with
with
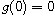 .
By using the variational method and the principle of symmetric criticality
for non-smooth Szulkin-type functionals, we establish that:
(1) the unperturbed problem, i.e. with
.
By using the variational method and the principle of symmetric criticality
for non-smooth Szulkin-type functionals, we establish that:
(1) the unperturbed problem, i.e. with
 has infinitely many
solutions;
(2) the number of distinct solutions becomes greater and greater when
has infinitely many
solutions;
(2) the number of distinct solutions becomes greater and greater when
 is smaller and smaller. Moreover, various properties of the
solutions are also described in terms of the
is smaller and smaller. Moreover, various properties of the
solutions are also described in terms of the
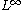 -
and
-
and
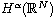 -norms.
-norms.

