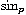 with p an integer greater than 2
with p an integer greater than 2
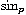 with p an integer greater than 2
with p an integer greater than 2
Lukas Kotrla
Abstract:
We find an explicit formula for the coefficients of the generalized
Maclaurin series for
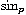 provided p>2 is an integer.
Our method is based on an expression of the
provided p>2 is an integer.
Our method is based on an expression of the
 -th derivative of
-th derivative of
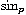 in the form
in the form
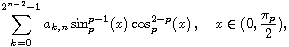
where \cos_p stands for the first derivative of
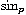 .
The formula allows us to compute the nonzero coefficients
.
The formula allows us to compute the nonzero coefficients

Submitted April 24, 2017. Published July 1, 2018.
Math Subject Classifications: 34L10, 33E30, 33F05.
Key Words: p-Laplacian; p-trigonometry; approximation;
analytic function coefficients of Maclaurin series.
Show me the PDF file (243 KB), TEX file for this article.
 |
Lukas Kotrla Department of Mathematics and NTIS Faculty of Applied Scences, University of West Bohemia Univerzitni 22, CZ-306 14 Plzen, Czech Republic email: kotrla@kma.zcu.cz |
|---|
Return to the EJDE web page