Electron. J. Differential Equations,
Vol. 2018 (2018), No. 150, pp. 1-6.
Existence and uniqueness of solutions for a second-order
iterative boundary-value problem
Eric R. Kaufmann
Abstract:
We consider the existence and uniqueness of solutions to the second-order
iterative boundary-value problem
![$$
x''(t) = f(t, x(t), x^{[2]}(t)), \quad a \leq t \leq b,
$$](images/aa.png)
where
![$x^{[2]}(t) = x(x(t))$](images/ab.png) , with solutions satisfying one of the
boundary conditions
, with solutions satisfying one of the
boundary conditions
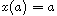 ,
,
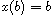 or
or
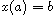 ,
,
 .
The main tool employed to establish our results is the Schauder fixed
point theorem.
.
The main tool employed to establish our results is the Schauder fixed
point theorem.
Submitted September 20 2017. Published August 8, 2018.
Math Subject Classifications: 34B15, 34K10, 39B05.
Key Words: Iterative differential equation; Schauder fixed point theorem;
contraction mapping principle.
Show me the PDF file (176 KB),
TEX file for this article.
 |
Eric R. Kaufmann
Department of Mathematics & Statistics
University of Arkansas at Little Rock
Little Rock, AR 72204, USA
email: erkaufmann@ualr.edu
|
|---|
Return to the EJDE web page
![$$
x''(t) = f(t, x(t), x^{[2]}(t)), \quad a \leq t \leq b,
$$](images/aa.png)
![$x^{[2]}(t) = x(x(t))$](images/ab.png) , with solutions satisfying one of the
boundary conditions
, with solutions satisfying one of the
boundary conditions
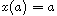 ,
,
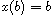 or
or
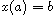 ,
,
 .
The main tool employed to establish our results is the Schauder fixed
point theorem.
.
The main tool employed to establish our results is the Schauder fixed
point theorem.
