Electron. J. Differential Equations,
Vol. 2018 (2018), No. 178, pp. 1-14.
Positive solution curves of an infinite semipositone problem
Rajendran Dhanya
Abstract:
In this article we consider the infinite semipositone problem
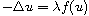 in
in
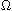 ,
a smooth bounded domain in
,
a smooth bounded domain in
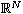 ,
and u=0 on
,
and u=0 on
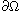 ,
where
,
where
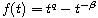 and
and
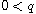 ,
,
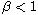 .
Using stability analysis we prove the existence of a connected branch
of maximal solutions emanating from infinity. Under certain additional
hypothesis on the extremal solution at
.
Using stability analysis we prove the existence of a connected branch
of maximal solutions emanating from infinity. Under certain additional
hypothesis on the extremal solution at
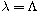 we prove a version
of Crandall-Rabinowitz bifurcation theorem which provides a multiplicity
result for
we prove a version
of Crandall-Rabinowitz bifurcation theorem which provides a multiplicity
result for
 .
.
Submitted May 3, 2018. Published November 1, 2018.
Math Subject Classifications: 35J25, 35J61, 35J75.
Key Words: Semipositone problems; topological methods; bifurcation theory.
Show me the PDF file (280 KB),
TEX file for this article.
Rajendran Dhanya
School of Mathematics and Computer Science
Indian Institute of Technology
Goa 403401, India
email: dhanya.tr@gmail.com
|
Return to the EJDE web page
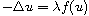 in
in
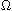 ,
a smooth bounded domain in
,
a smooth bounded domain in
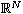 ,
and u=0 on
,
and u=0 on
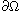 ,
where
,
where
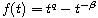 and
and
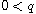 ,
,
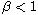 .
Using stability analysis we prove the existence of a connected branch
of maximal solutions emanating from infinity. Under certain additional
hypothesis on the extremal solution at
.
Using stability analysis we prove the existence of a connected branch
of maximal solutions emanating from infinity. Under certain additional
hypothesis on the extremal solution at
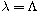 we prove a version
of Crandall-Rabinowitz bifurcation theorem which provides a multiplicity
result for
we prove a version
of Crandall-Rabinowitz bifurcation theorem which provides a multiplicity
result for
 .
.