Electron. J. Differential Equations,
Vol. 2018 (2018), No. 193, pp. 1-13.
Infinite semipositone problems with a falling zero and
nonlinear boundary conditions
Mohan Mallick, Lakshmi Sankar, Ratnasingham Shivaji, Subbiah Sundar
Abstract:
We consider the problem
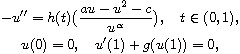
where
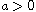 ,
,
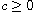 ,
,
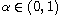 ,
,
![$h{:}(0, 1] \to (0, \infty)$](images/ae.png) is a continuous function which may be singular at
is a continuous function which may be singular at
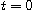 ,
but belongs to
,
but belongs to
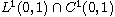 , and
, and
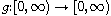 is a continuous
function. We discuss existence, uniqueness, and non existence results for
positive solutions for certain values of a, b and c.
is a continuous
function. We discuss existence, uniqueness, and non existence results for
positive solutions for certain values of a, b and c.
Submitted October 15, 2018. Published November 27, 2018.
Math Subject Classifications: 35J25, 35J66. 35J75.
Key Words: Infinite semipostione; exterior domain; sub and super solutions;
nonlinear boundary conditions.
Show me the PDF file (1194 KB),
TEX file for this article.
 |
Mohan Mallick
Department of Mathematics
IIT Madras, Chennai-600036, India
email: mohan.math09@gmail.com
|
|---|
 |
Lakshmi Sankar
Department of Mathematics
IIT Palakkad, Kerala-678557, India
email: lakshmi@iitpkd.ac.in
|
|---|
 |
Ratnasingham Shivaji
Department of Mathematics and Statistics
University of North Carolina at
Greensboro, NC 27412, USA
email: shivaji@uncg.edu
|
|---|
 |
Subbiah Sundar
Department of Mathematics
IIT Madras, Chennai-600036, India
email: slnt@iitm.ac.in
|
|---|
Return to the EJDE web page
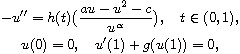
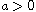 ,
,
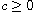 ,
,
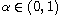 ,
,
![$h{:}(0, 1] \to (0, \infty)$](images/ae.png) is a continuous function which may be singular at
is a continuous function which may be singular at
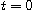 ,
but belongs to
,
but belongs to
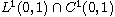 , and
, and
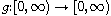 is a continuous
function. We discuss existence, uniqueness, and non existence results for
positive solutions for certain values of a, b and c.
is a continuous
function. We discuss existence, uniqueness, and non existence results for
positive solutions for certain values of a, b and c.



