Electron. J. Differential Equations,
Vol. 2018 (2018), No. 27, pp. 1-15.
Composition and convolution theorems for mu-Stepanov pseudo almost periodic
functions and applications to fractional integro-differential equations
Edgardo Alvarez
Abstract:
In this article we establish new convolution and composition theorems
for
 -Stepanov pseudo almost periodic functions.
We prove that the space of vector-valued mu-Stepanov pseudo almost
periodic functions is a Banach space.
As an application, we prove the existence and uniqueness of
mu-pseudo almost periodic mild solutions for the fractional
integro-differential equation
-Stepanov pseudo almost periodic functions.
We prove that the space of vector-valued mu-Stepanov pseudo almost
periodic functions is a Banach space.
As an application, we prove the existence and uniqueness of
mu-pseudo almost periodic mild solutions for the fractional
integro-differential equation
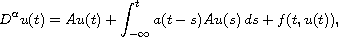
where A generates an
 -resolvent family
-resolvent family
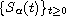 on a Banach space X,
on a Banach space X,
 ,
,
 ,
the fractional derivative is understood in the sense of Weyl and the
nonlinearity f is a mu-Stepanov pseudo almost periodic function.
,
the fractional derivative is understood in the sense of Weyl and the
nonlinearity f is a mu-Stepanov pseudo almost periodic function.
Submitted September 12, 2016. Published January 18, 2018.
Math Subject Classifications: 45D05, 34A12, 45N05.
Key Words: mu-Stepanov pseudo almost periodic; mild solutions,;
fractional integro-differential equations; composition; convolution.
Show me the PDF file (268 KB),
TEX file for this article.
 |
Edgardo Alvarez
Universidad del Norte
Departamento de Matemáticas y Estadística
Barranquilla, Colombia
email: edgalp@yahoo.com, ealvareze@uninorte.edu.co
|
|---|
Return to the EJDE web page
 -Stepanov pseudo almost periodic functions.
We prove that the space of vector-valued mu-Stepanov pseudo almost
periodic functions is a Banach space.
As an application, we prove the existence and uniqueness of
mu-pseudo almost periodic mild solutions for the fractional
integro-differential equation
-Stepanov pseudo almost periodic functions.
We prove that the space of vector-valued mu-Stepanov pseudo almost
periodic functions is a Banach space.
As an application, we prove the existence and uniqueness of
mu-pseudo almost periodic mild solutions for the fractional
integro-differential equation
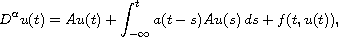
 -resolvent family
-resolvent family
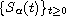 on a Banach space X,
on a Banach space X,
 ,
,
 ,
the fractional derivative is understood in the sense of Weyl and the
nonlinearity f is a mu-Stepanov pseudo almost periodic function.
,
the fractional derivative is understood in the sense of Weyl and the
nonlinearity f is a mu-Stepanov pseudo almost periodic function.
