Electron. J. Differential Equations,
Vol. 2018 (2018), No. 35, pp. 1-16.
Dirichlet boundary value problem for a system of n
second order asymptotically asymmetric differential equations
Armands Gritsans, Felix Sadyrbaev, Inara Yermachenko
Abstract:
We consider systems of the form

along with the boundary conditions
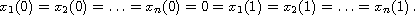
We assume that right sides are bounded continuous functions, and satisfy
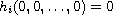 . Also we assume that
. Also we assume that
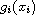 are asymptotically asymmetric functions.
By using vector field rotation theory, we provide the existence
of solutions.
are asymptotically asymmetric functions.
By using vector field rotation theory, we provide the existence
of solutions.
Submitted April 5, 2017. Published January 24, 2018.
Math Subject Classifications: 34B08, 34B15.
Key Words: Dirichlet boundary value problem; rotation of vector field;
asymptotically asymmetric nonlinearities;
index of isolated singular point; Fucik spectrum.
Show me the PDF file (453 KB),
TEX file for this article.
 |
Armands Gritsans
Institute of Life Sciences and Technologies
Daugavpils University
Parades iela 1a, Daugavpils LV 5400, Latvia
email: arminge@inbox.lv
|
|---|
 |
Felix Sadyrbaev
Institute of Life Sciences and Technologies
Daugavpils University
Parades iela 1a, Daugavpils LV 5400, Latvia
email: felix@latnet.lv
|
|---|
 |
Inara Yermachenko
Institute of Life Sciences and Technologies
Daugavpils University
Parades iela 1a, Daugavpils LV 5400, Latvia
email: inara.jermacenko@du.lv
|
|---|
Return to the EJDE web page

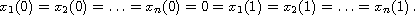
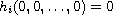 . Also we assume that
. Also we assume that
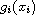 are asymptotically asymmetric functions.
By using vector field rotation theory, we provide the existence
of solutions.
are asymptotically asymmetric functions.
By using vector field rotation theory, we provide the existence
of solutions.


