Electron. J. Differential Equations,
Vol. 2018 (2018), No. 45, pp. 1-23.
Nonlinear anisotropic elliptic equations with variable exponents and
degenerate coercivity
Hocine Ayadi, Fares Mokhtari
Abstract:
In this article, we prove the existence and the regularity of distributional
solutions for a class of nonlinear anisotropic elliptic equations with
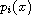 growth conditions, degenerate coercivity and
growth conditions, degenerate coercivity and
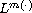 data,
with
data,
with
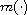 being small, in appropriate Lebesgue-Sobolev spaces with
variable exponents. The obtained results extend some existing ones [8,10].
being small, in appropriate Lebesgue-Sobolev spaces with
variable exponents. The obtained results extend some existing ones [8,10].
Submitted May 18, 2017. Published February 12, 2018.
Math Subject Classifications: 35J70, 35J60, 35B65.
Key Words: Anisotropic elliptic equations; variable exponents;
degenerate coercivity; distributional solutions;
irregular data
Show me the PDF file (345 KB),
TEX file for this article.
 |
Hocine Ayadi
Département de mathématiques
Université Mohamed Boudiaf-M'sila
BP 166 M'sila 28000, Algeria
email: ayadi.hocine@yahoo.fr
|
|---|
 |
Fares Mokhtari
Département de Mathématiques et Informatique
Université Benyoucef Benkhedda
Alger 1, 2 Rue Didouche Mourad, Algeria
email: fares_maths@yahoo.fr
|
|---|
Return to the EJDE web page
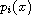 growth conditions, degenerate coercivity and
growth conditions, degenerate coercivity and
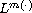 data,
with
data,
with
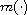 being small, in appropriate Lebesgue-Sobolev spaces with
variable exponents. The obtained results extend some existing ones [8,10].
being small, in appropriate Lebesgue-Sobolev spaces with
variable exponents. The obtained results extend some existing ones [8,10].

