Electron. J. Differential Equations,
Vol. 2018 (2018), No. 67, pp. 1-14.
Radial solutions for inhomogeneous biharmonic elliptic systems
Reginaldo Demarque, Narciso da Hora Lisboa
Abstract:
In this article we obtain weak radial solutions for the
inhomogeneous elliptic system
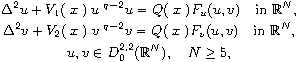
where
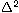 is the biharmonic operator,
is the biharmonic operator,
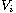 ,
,
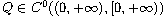 , i=1,2, are radially
symmetric potentials,
, i=1,2, are radially
symmetric potentials,
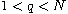 ,
,
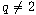 ,
and F is a s-homogeneous function.
Our approach relies on an application of the Symmetric Mountain Pass
Theorem and a compact embedding result proved in [17].
,
and F is a s-homogeneous function.
Our approach relies on an application of the Symmetric Mountain Pass
Theorem and a compact embedding result proved in [17].
Submitted June 16, 2017. Published March 14, 2018.
Math Subject Classifications: 35J50, 31A30.
Key Words: Biharmonic operator; elliptic systems; existence of solutions;
radial solution; mountain pass theorem.
Show me the PDF file (353 KB),
TEX file for this article.
 |
Reginaldo Demarque
Departamento de Ciências da Natureza
Universidade Federal Fluminense
Rio das Ostras, RJ, 28895-532, Brazil
email: r.demarque@gmail.com
|
|---|
 |
Narciso da Hora Lisboa
Departamento de Ciências Exatas
Universidade Estadual de Montes Claros
Montes Claros, MG, 39401-089, Brazil
email: narciso.lisboa@unimontes.br
|
|---|
Return to the EJDE web page
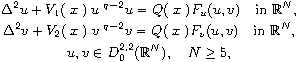
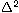 is the biharmonic operator,
is the biharmonic operator,
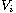 ,
,
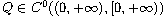 , i=1,2, are radially
symmetric potentials,
, i=1,2, are radially
symmetric potentials,
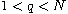 ,
,
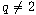 ,
and F is a s-homogeneous function.
Our approach relies on an application of the Symmetric Mountain Pass
Theorem and a compact embedding result proved in [17].
,
and F is a s-homogeneous function.
Our approach relies on an application of the Symmetric Mountain Pass
Theorem and a compact embedding result proved in [17].

