Electron. J. Differential Equations,
Vol. 2018 (2018), No. 71, pp. 1-11.
Stable solutions to weighted quasilinear problems of Lane-Emden type
Phuong Le, Vu Ho
Abstract:
We prove that all entire stable
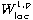 solutions of weighted
quasilinear problem
solutions of weighted
quasilinear problem

must be zero. The result holds true for
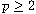 and
and
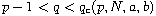 .
Here
.
Here
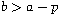 and
and
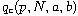 is a new critical exponent, which is
infinity in low dimension and is always larger than the classic critical one,
while
is a new critical exponent, which is
infinity in low dimension and is always larger than the classic critical one,
while
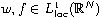 are nonnegative functions such
that
are nonnegative functions such
that
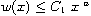 and
and
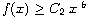 for large |x|.
We also construct an example to show the sharpness of our result.
for large |x|.
We also construct an example to show the sharpness of our result.
Submitted July 11, 2017. Published March 15, 2018.
Math Subject Classifications: 35B53, 35J92, 35B08, 35B35.
Key Words: Quasilinear problems; stable solutions; Lane-Emden nonlinearity;
Liouville theorems.
Show me the PDF file (342 KB),
TEX file for this article.
 |
Phuong Le
Department of Mathematical Economics
Banking University of Ho Chi Minh City, Vietnam
email: phuongl@buh.edu.vn
|
|---|
 |
Vu Ho
Division of Computational Mathematics and Engineering
Institute for Computational Science
Ton Duc Thang University, Ho Chi Minh City, Vietnam
email: hovu@tdt.edu.vn
|
|---|
Return to the EJDE web page
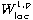 solutions of weighted
quasilinear problem
solutions of weighted
quasilinear problem

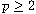 and
and
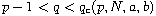 .
Here
.
Here
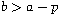 and
and
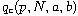 is a new critical exponent, which is
infinity in low dimension and is always larger than the classic critical one,
while
is a new critical exponent, which is
infinity in low dimension and is always larger than the classic critical one,
while
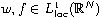 are nonnegative functions such
that
are nonnegative functions such
that
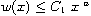 and
and
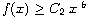 for large |x|.
We also construct an example to show the sharpness of our result.
for large |x|.
We also construct an example to show the sharpness of our result.

