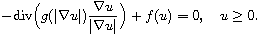Electron. J. Differential Equations,
Vol. 2018 (2018), No. 91, pp. 1-9.
Harnack inequality for quasilinear elliptic equations with (p,q)
growth conditions and absorption lower order term
Kateryna Buryachenko
Abstract:
In this article we study the quasilinear elliptic equation with absorption
lower term
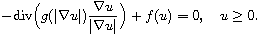
Despite of the lack of comparison principle, we prove a priori
estimate of Keller-Osserman type. Particularly, under some natural
assumptions on the functions g,f for nonnegative solutions we
prove an estimate of the form
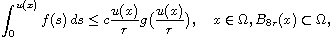
with constant c, independent on u(x). Using this estimate we
give a simple proof of the Harnack inequality.
Submitted June 14, 2017. Published April 16, 2018.
Math Subject Classifications: 35J15, 35J60, 35J62.
Key Words: Harnack inequality; quasilinear elliptic equation;
Keller-Osserman type estimate; absorption lower term.
Show me the PDF file (247 KB),
TEX file for this article.
 |
Kateryna Buryachenko
Vasyl' Stus Donetsk National University
600-richa Str., 21
Vinnytsia, 21021, Ukraine
email: katarzyna_@ukr.net
|
|---|
Return to the EJDE web page