Electron. J. Differential Equations,
Vol. 2019 (2019), No. 25, pp. 1-22.
Stable manifolds for impulsive delay equations and parameter dependence
Dhirendra Bahuguna, Lokesh Singh
Abstract:
In this article, we establish the existence of Lipschitz stable invariant
manifolds for the semiflows generated by the delay differential equation
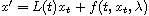 with impulses at times
with impulses at times
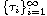 , assuming that the perturbation
, assuming that the perturbation
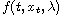 as well as the impulses are small and the corresponding linear delay
differential equation admits a nonuniform exponential dichotomy.
We also show that the obtained manifolds are Lipschitz in the parameter
as well as the impulses are small and the corresponding linear delay
differential equation admits a nonuniform exponential dichotomy.
We also show that the obtained manifolds are Lipschitz in the parameter
 .
.
Submitted April 3, 2018. Published February 13, 2019.
Math Subject Classifications: 37D10, 34D09, 37D25, 35R10, 35R12.
Key Words: Delay impulsive equation; exponential dichotomy;
stable invariant manifold.
Show me the PDF file (305 KB),
TEX file for this article.
 |
Dhirendra Bahuguna
Department of Mathematics and Statistics
Indian Institute of Technology
Kanpur-208016, India
email: dhiren@iitk.ac.in
|
|---|
 |
Lokesh Singh
Department of Mathematics and Statistics
Indian Institute of Technology
Kanpur-208016, India
email: lokesh@iitk.ac.in
|
|---|
Return to the EJDE web page
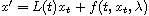 with impulses at times
with impulses at times
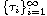 , assuming that the perturbation
, assuming that the perturbation
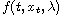 as well as the impulses are small and the corresponding linear delay
differential equation admits a nonuniform exponential dichotomy.
We also show that the obtained manifolds are Lipschitz in the parameter
as well as the impulses are small and the corresponding linear delay
differential equation admits a nonuniform exponential dichotomy.
We also show that the obtained manifolds are Lipschitz in the parameter
 .
.

