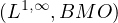
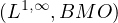
Nguyen Anh Dao, Nguyen Thi Ngoc Hanh,Tran Minh Hieu, Huy Bac Nguyen
Abstract:
We prove interpolation inequalities by means of the Lorentz norm,
BMO norm, and the fractional Sobolev norm. In particular, we obtain
an interpolation inequality for
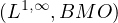 ,
that we call
the endpoint case.
,
that we call
the endpoint case.
Submitted February 6, 2019. Published May 3, 2019.
Math Subject Classifications: 46E35, 26D10.
Key Words: Gagliardo-Nirenberg inequality; Lorentz spaces; BMO space;
Fractional Sobolev spaces.
Show me the PDF file (297 KB), TEX file for this article.
| Nguyen Anh Dao Applied Analysis Research Group Faculty of Mathematics and Statistics Ton Duc Thang University Ho Chi Minh City, Vietnam email: daonguyenanh@tdtu.edu.vn | |
 |
Nguyen Thi Ngoc Hanh Le Loi High school Gia Lai Province, Vietnam email: nguyenthingochanh.thptleloi@gmail.com |
 |
Tran Minh Hieu Luong The Vinh High school Gia Lai Province. Vietnam email: tranhieukbang@gmail.com |
 |
Huy Bac Nguyen Faculty of Electrical Engineering & Computer Science Technical University of Ostrava Czech Republic email: huy.bac.nguyen.st@vsb.cz |
Return to the EJDE web page