In this article, we prove the existence of multiple nontrivial solutions to the equation
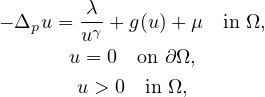
where
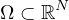 is a smooth bounded domain with
is a smooth bounded domain with
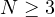 ,
,
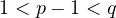 ,
,
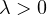 ,
,
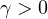 ,
g satisfies
certain conditions,
,
g satisfies
certain conditions,
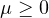 is a bounded Radon measure.
is a bounded Radon measure.
Sekhar Ghosh, Akasmika Panda, Debajyoti Choudhuri
Abstract:
In this article, we prove the existence of multiple nontrivial solutions
to the equation
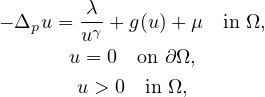
where
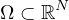 is a smooth bounded domain with
is a smooth bounded domain with
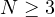 ,
,
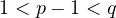 ,
,
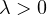 ,
,
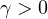 ,
g satisfies
certain conditions,
,
g satisfies
certain conditions,
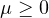 is a bounded Radon measure.
is a bounded Radon measure.
Submitted April 16, 2018. Published May 6, 2019.
Math Subject Classifications: 35J60, 35J75, 35R06.
Key Words: Elliptic PDEs; p-Laplacian; Radon measure
Show me the PDF file (395 KB), TEX file for this article.
 |
Sekhar Ghosh Department of Mathematics National Institute of Technology Rourkela, India email: sekharghosh1234@gmail.com |
|---|---|
 |
Akasmika Panda Department of Mathematics National Institute of Technology Rourkela, India email: akasmika44@gmail.com |
 |
Debajyoti Choudhuri Department of Mathematics National Institute of Technology Rourkela, India email: dc.iit12@gmail.com |
Return to the EJDE web page