Electron. J. Differential Equations,
Vol. 2019 (2019), No. 67, pp. 1-15.
A Brezis-Nirenberg problem on hyperbolic spaces
Paulo Cesar Carriao, Raquel Lehrer, Olimpio Hiroshi Miyagaki, Andre Vicente
Abstract:
We consider a Brezis-Nirenberg problem on the hyperbolic space
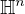 .
By using the stereographic projection, the problem becomes a singular
problem on the boundary of the open ball
.
By using the stereographic projection, the problem becomes a singular
problem on the boundary of the open ball
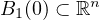 .
Thanks to the Hardy inequality, in a version due to Brezis-Marcus,
the difficulty involving singularities can be overcame.
We use the mountain pass theorem due to Ambrosetti-Rabinowitz and
Brezis-Nirenberg arguments to obtain a nontrivial solution.
.
Thanks to the Hardy inequality, in a version due to Brezis-Marcus,
the difficulty involving singularities can be overcame.
We use the mountain pass theorem due to Ambrosetti-Rabinowitz and
Brezis-Nirenberg arguments to obtain a nontrivial solution.
Submitted June 30, 2018. Published May 13, 2019.
Math Subject Classifications: 32Q45, 35A15, 35B38, 35B33.
Key Words: Variational method; critical point; critical exponent; hyperbolic manifold.
Show me the PDF file (369 KB),
TEX file for this article.
 |
Paulo César Carrião
Universidade Federal de Minas Gerais
- ICEX - DM, CEP: 31270-901
Belo Horizonte, MG, Brazil
email: pauloceca@gmail.com
|
|---|
 |
Raquel Lehrer
Universidade Estadual do Oeste do Paraná - CCET
Rua Universitária, 2069
Jd. Universitário, CEP: 85819-110
Cascavel, PR, Brazil
email: rlehrer@gmail.com
|
|---|
 |
Olíimpio Hiroshi Miyagaki
Universidade Federal de Juiz de Fora - DM
CEP: 36036-330
Juiz de Fora, MG, Brazil
email: ohmiyagaki@gmail.com
|
|---|
 |
André Vicente
Universidade Estadual do Oeste do Paraná - CCET
Rua Universitária, 2069
Jd. Universitário
CEP: 85819-110
Cascavel, PR, Brazil
email: andre.vicente@unioeste.br
|
|---|
Return to the EJDE web page
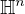 .
By using the stereographic projection, the problem becomes a singular
problem on the boundary of the open ball
.
By using the stereographic projection, the problem becomes a singular
problem on the boundary of the open ball
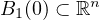 .
Thanks to the Hardy inequality, in a version due to Brezis-Marcus,
the difficulty involving singularities can be overcame.
We use the mountain pass theorem due to Ambrosetti-Rabinowitz and
Brezis-Nirenberg arguments to obtain a nontrivial solution.
.
Thanks to the Hardy inequality, in a version due to Brezis-Marcus,
the difficulty involving singularities can be overcame.
We use the mountain pass theorem due to Ambrosetti-Rabinowitz and
Brezis-Nirenberg arguments to obtain a nontrivial solution.



