Electron. J. Differential Equations,
Vol. 2019 (2019), No. 72, pp. 1-19.
Non-autonomous approximations governed by the fractional powers
of damped wave operators
Marcelo J. D. Nascimento, Flank D. M. Bezerra
Abstract:
In this article we study non-autonomous approximations governed by the
fractional powers of damped wave operators of order
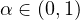 subject to Dirichlet boundary conditions in an
subject to Dirichlet boundary conditions in an
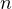 -dimensional bounded
domain with smooth boundary. We give explicitly expressions for the
fractional powers of the wave operator, we compute their resolvent
operators and their eigenvalues. Moreover, we study the convergence
as
-dimensional bounded
domain with smooth boundary. We give explicitly expressions for the
fractional powers of the wave operator, we compute their resolvent
operators and their eigenvalues. Moreover, we study the convergence
as
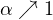 with rate
with rate
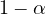 .
.
Submitted January 24, 2019. Published May 17, 2019.
Math Subject Classifications: 35L05, 35B40.
Key Words: Non-autonomous damped wave equations; fractional powers;
rate of convergence; eigenvalues.
Show me the PDF file (377 KB),
TEX file for this article.
 |
Marcelo J. D. Nascimento
Universidade Federal de São
Carlos, Departamento de Matemática
13565-905 São, Carlos SP, Brazil
email: marcelo@dm.ufscar.br
|
|---|
 |
Flank D. M. Bezerra
Departamento de Matemática
Universidade Federal da Paraíba
58051-900 João Pessoa PB, Brazil
email: flank@mat.ufpb.br
|
|---|
Return to the EJDE web page
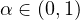 subject to Dirichlet boundary conditions in an
subject to Dirichlet boundary conditions in an
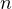 -dimensional bounded
domain with smooth boundary. We give explicitly expressions for the
fractional powers of the wave operator, we compute their resolvent
operators and their eigenvalues. Moreover, we study the convergence
as
-dimensional bounded
domain with smooth boundary. We give explicitly expressions for the
fractional powers of the wave operator, we compute their resolvent
operators and their eigenvalues. Moreover, we study the convergence
as
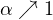 with rate
with rate
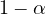 .
.

