Let T be a strongly continuous semigroup acting on a complex Banach space X and let A be its infinitesimal generator. It is well-known [29,33] that the uniform spectral bound
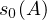 of the semigroup T is negative provided that all solutions to
the Cauchy problems
of the semigroup T is negative provided that all solutions to
the Cauchy problems
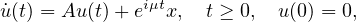
are bounded (uniformly with respect to the parameter
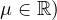 .
In particular, if X is a Hilbert space, then this yields all trajectories
of the semigroup T are exponentially stable, but if X is an
arbitrary Banach space this result is no longer valid. Let
.
In particular, if X is a Hilbert space, then this yields all trajectories
of the semigroup T are exponentially stable, but if X is an
arbitrary Banach space this result is no longer valid. Let
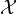 denote the space of all continuous and 1-periodic functions
denote the space of all continuous and 1-periodic functions
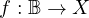 whose sequence of Fourier-Bohr coefficients
whose sequence of Fourier-Bohr coefficients
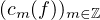 belongs to
belongs to
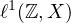 .
Endowed with the norm
.
Endowed with the norm
 it becomes
a non-reflexive Banach space [15].
A subspace
it becomes
a non-reflexive Banach space [15].
A subspace
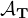 of X (related to the pair
of X (related to the pair
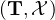 ) is introduced in the third section of this paper.
We prove that the semigroup T is uniformly exponentially stable
provided that in addition to the above-mentioned boundedness condition,
) is introduced in the third section of this paper.
We prove that the semigroup T is uniformly exponentially stable
provided that in addition to the above-mentioned boundedness condition,
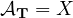 .
An example of a strongly continuous semigroup (which is not uniformly continuous)
and fulfills the second assumption above is also provided. Moreover an
extension of the above result from semigroups to 1-periodic and strongly
continuous evolution families acting in a Banach space is given.
We also prove that the evolution semigroup
.
An example of a strongly continuous semigroup (which is not uniformly continuous)
and fulfills the second assumption above is also provided. Moreover an
extension of the above result from semigroups to 1-periodic and strongly
continuous evolution families acting in a Banach space is given.
We also prove that the evolution semigroup
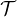 associated with T on
associated with T on
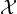 does not verify the spectral determined growth
condition. More precisely, an example of such a semigroup with uniform spectral
bound negative and uniformly growth bound non-negative is given.
Finally we prove that the assumption
does not verify the spectral determined growth
condition. More precisely, an example of such a semigroup with uniform spectral
bound negative and uniformly growth bound non-negative is given.
Finally we prove that the assumption
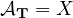 is not
needed in the discrete case.
is not
needed in the discrete case.



