Electron. J. Differential Equations, Vol. 2020 (2020), No. 105, pp. 1-15.
Nonlinear degenerate elliptic equations in weighted Sobolev spaces
Aharrouch Benali, Bennouna Jaouad
Abstract:
We study the existence of solutions for the nonlinear degenerated elliptic problem
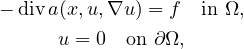
where
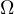 is a bounded open set in
is a bounded open set in
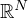 ,
,
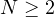 , a is a Caratheodory
function having degenerate coercivity
, a is a Caratheodory
function having degenerate coercivity
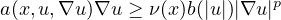 ,
1<p<N,
,
1<p<N,
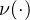 is the weight function,
b is continuous and
is the weight function,
b is continuous and
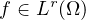 .
.
Submitted December 4, 2019. Published October 12, 2020.
Math Subject Classifications: 35J70, 46E30, 35J85.
Key Words: Nonlinear degenerated elliptic operators; weighted Sobolev space;
monotony and rearrangement methods.
DOI: 10.58997/ejde.2020.105
Show me the PDF file (350 KB),
TEX file for this article.
 |
Aharrouch Benali
Sidi Mohamed Ben Abdellah University
Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics
P.O. Box 1796 Atlas Fez, Morocco
email: bnaliaharrouch@gmail.com
|
|---|
 |
Bennouna Jaouad
Sidi Mohamed Ben Abdellah University
Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics
P.O. Box 1796 Atlas Fez, Morocco
email: jbennouna@hotmail.com
|
|---|
Return to the EJDE web page
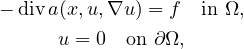
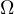 is a bounded open set in
is a bounded open set in
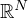 ,
,
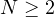 , a is a Caratheodory
function having degenerate coercivity
, a is a Caratheodory
function having degenerate coercivity
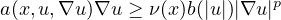 ,
1<p<N,
,
1<p<N,
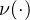 is the weight function,
b is continuous and
is the weight function,
b is continuous and
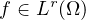 .
.

