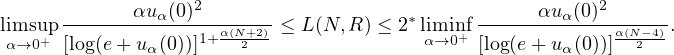Electron. J. Differential Equations, Vol. 2020 (2020), No. 114, pp. 1-17.
Asymptotic behavior of positive radial solutions to elliptic equations
approaching critical growth
Rosa Pardo, Arturo Sanjuan
Abstract:
We study the asymptotic behavior of radially symmetric solutions
to the subcritical semilinear elliptic problem
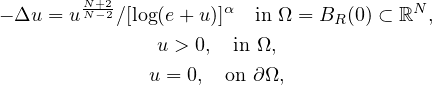
as
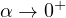 .
Using asymptotic estimates, we prove that there exists an explicitly defined constant
L(N,R)>0, only depending on N and R, such that
.
Using asymptotic estimates, we prove that there exists an explicitly defined constant
L(N,R)>0, only depending on N and R, such that
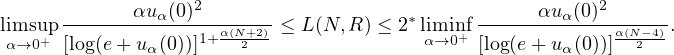
Submitted November 11, 2019. Published November 18, 2020.
Math Subject Classifications: 35B33, 35B45, 35B09, 35J60.
Key Words: A priori bounds; positive solutions; semilinear elliptic equations;
Dirichlet boundary conditions; growth estimates; subcritical nonlinearites.
DOI: 10.58997/ejde.2020.114
Show me the PDF file (391 KB),
TEX file for this article.
 |
Rosa Pardo
Universidad Complutense de Madrid
28040 Madrid, Spain
email: rpardo@ucm.es
|
|---|
 |
Arturo Sanjuán
Universidad Distrital Francisco José de Caldas
Bogotá, Colombia
email: aasanjuanc@udistrital.edu.co
|
|---|
Return to the EJDE web page
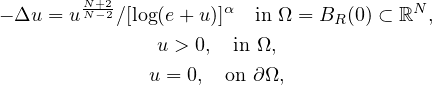
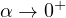 .
Using asymptotic estimates, we prove that there exists an explicitly defined constant
L(N,R)>0, only depending on N and R, such that
.
Using asymptotic estimates, we prove that there exists an explicitly defined constant
L(N,R)>0, only depending on N and R, such that