Electron. J. Differential Equations, Vol. 2020 (2020), No. 29, pp. 1-12.
Existence of solutions to fractional Hamiltonian systems with
local superquadratic conditions
Zijun Guo, Qingye Zhang
Abstract:
In this article, we study the existence of solutions for the fractional
Hamiltonian system
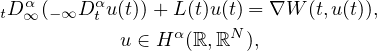
where
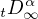 and
and
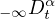 are the Liouville-Weyl
fractional derivatives of order
are the Liouville-Weyl
fractional derivatives of order
 ,
,
 is a symmetric matrix-valued function,
which is unnecessarily required to be coercive,
and
is a symmetric matrix-valued function,
which is unnecessarily required to be coercive,
and
 satisfies some kind of
local superquadratic conditions, which is rather weaker than the usual
Ambrosetti-Rabinowitz condition.
satisfies some kind of
local superquadratic conditions, which is rather weaker than the usual
Ambrosetti-Rabinowitz condition.
Submitted September 21, 2019. Published April 6, 2020.
Math Subject Classifications: 26A33, 35A15, 35B38, 37J45.
Key Words: Fractional Hamiltonian system; variational method; superquadratic.
DOI: 10.58997/ejde.2020.29
Show me the PDF file (356 KB),
TEX file for this article.
 |
Zijun Guo
College of Mathematics and Information Science
Jiangxi Normal University
Nanchang 330022, China
email: 1095752878@qq.com
|
|---|
 |
Qingye Zhang
College of Mathematics and Information Science
Jiangxi Normal University
Nanchang 330022, China
email: qingyezhang@gmail.com
|
|---|
Return to the EJDE web page
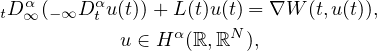
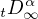 and
and
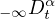 are the Liouville-Weyl
fractional derivatives of order
are the Liouville-Weyl
fractional derivatives of order
 ,
,
 is a symmetric matrix-valued function,
which is unnecessarily required to be coercive,
and
is a symmetric matrix-valued function,
which is unnecessarily required to be coercive,
and
 satisfies some kind of
local superquadratic conditions, which is rather weaker than the usual
Ambrosetti-Rabinowitz condition.
satisfies some kind of
local superquadratic conditions, which is rather weaker than the usual
Ambrosetti-Rabinowitz condition.

