Electron. J. Differential Equations,
Vol. 2020 (2020), No. 45, pp. 1-15.
Positive solutions for a nonlinear system of fourth-order ordinary
differential equations
Qiuyue Wang, Lu Yang
Abstract:
In this article, we consider the existence of positive solutions for a nonlinear
system of fourth-order ordinary differential equations. By constructing a single
cone
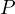 in the product space
in the product space
![$C[0, 1] \times C[0, 1]$](images/a1x.png) and applying fixed point
theorem in cones, we establish the existence of positive solutions for a system
in which the nonlinear terms are both superlinear or sublinear.
In addition, by the construction of the product cone
and applying fixed point
theorem in cones, we establish the existence of positive solutions for a system
in which the nonlinear terms are both superlinear or sublinear.
In addition, by the construction of the product cone
![$K_1 \times K_2\subset C[0, 1] \times C[0, 1]$](images/a2x.png) along with the product formula of fixed point
theory on a product cone, we investigate the existence of positive solutions
involving nonlinear terms, one uniformly superlinear or sublinear, and the other
locally uniformly sublinear or superlinear.
along with the product formula of fixed point
theory on a product cone, we investigate the existence of positive solutions
involving nonlinear terms, one uniformly superlinear or sublinear, and the other
locally uniformly sublinear or superlinear.
Submitted December 9, 2019. Published May 19, 2020.
Math Subject Classifications: 34B18, 47H11, 47N20.
Key Words: Positive solution; fixed point theory; ordinary differential equation.
DOI: 10.58997/ejde.2020.45
Show me the PDF file (322 KB),
TEX file for this article.
 |
Qiuyue Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: wangqy17@lzu.edu.cn
|
|---|
 |
Lu Yang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: yanglu@lzu.edu.cn
|
|---|
Return to the EJDE web page
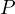 in the product space
in the product space
![$C[0, 1] \times C[0, 1]$](images/a1x.png) and applying fixed point
theorem in cones, we establish the existence of positive solutions for a system
in which the nonlinear terms are both superlinear or sublinear.
In addition, by the construction of the product cone
and applying fixed point
theorem in cones, we establish the existence of positive solutions for a system
in which the nonlinear terms are both superlinear or sublinear.
In addition, by the construction of the product cone
![$K_1 \times K_2\subset C[0, 1] \times C[0, 1]$](images/a2x.png) along with the product formula of fixed point
theory on a product cone, we investigate the existence of positive solutions
involving nonlinear terms, one uniformly superlinear or sublinear, and the other
locally uniformly sublinear or superlinear.
along with the product formula of fixed point
theory on a product cone, we investigate the existence of positive solutions
involving nonlinear terms, one uniformly superlinear or sublinear, and the other
locally uniformly sublinear or superlinear.

