Electron. J. Differential Equations, Vol. 2020 (2020), No. 47, pp. 1-10.
Positive solutions of Schrodinger-Poisson systems with Hardy
potential and indefinite nonlinearity
Yongyi Lan, Biyun Tang, Xian Hu
Abstract:
In this article, we study the nonlinear Schrodinger-Poisson system

where
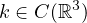 and 4<p<6, k changes sign in
and 4<p<6, k changes sign in
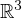 and
and
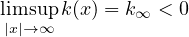 .
We prove that Schrodinger-Poisson systems with Hardy
potential and indefinite nonlinearity have at least one positive solution, using
variational methods.
.
We prove that Schrodinger-Poisson systems with Hardy
potential and indefinite nonlinearity have at least one positive solution, using
variational methods.
Submitted April 6, 2020. Published May 21, 2020.
Math Subject Classifications: 35J20, 35J70.
Key Words: Hardy potential; variational methods; indefinite nonlinearity;
positive solution.
DOI: 10.58997/ejde.2020.47
Show me the PDF file (320 KB),
TEX file for this article.
 |
Yongyi Lan
School of Science
Jimei University
Xiamen 61021, China
email: lanyongyi@jmu.edu.cn
|
|---|
 |
Biyun Tang
School of Science
Jimei University
Xiamen 61021, China
email: 1520840642@qq.com
|
|---|
 |
Xian Hu
School of Science
Jimei University
Xiamen 61021, China
email: 2321894958@qq.com
|
|---|
Return to the EJDE web page

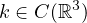 and 4<p<6, k changes sign in
and 4<p<6, k changes sign in
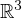 and
and
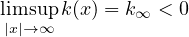 .
We prove that Schrodinger-Poisson systems with Hardy
potential and indefinite nonlinearity have at least one positive solution, using
variational methods.
.
We prove that Schrodinger-Poisson systems with Hardy
potential and indefinite nonlinearity have at least one positive solution, using
variational methods.


