Electron. J. Differential Equations, Vol. 2020 (2020), No. 60, pp. 1-15.
Existence and multiplicity for a superlinear elliptic problem under
a non-quadradicity condition at infinity
Leandro Recova, Adolfo Rumbos
Abstract:
In this article, we study the existence and multiplicity of solutions of the
boundary-value problem
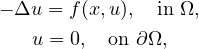
where
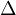 denotes the N-dimensional Laplacian,
denotes the N-dimensional Laplacian,
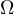 is a bounded domain
with smooth boundary,
is a bounded domain
with smooth boundary,
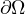 , in
, in
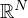
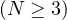 , and
f is a continuous function having subcritical growth in the second variable.
Using infinite-dimensional Morse theory, we extended the results of Furtado
and Silva [9]
by proving the existence of a second nontrivial solution under a non-quadradicity
condition at infinity on the non-linearity. Assuming more regularity on the
non-linearity f, we are able to prove the existence of at least three nontrivial
solutions.
, and
f is a continuous function having subcritical growth in the second variable.
Using infinite-dimensional Morse theory, we extended the results of Furtado
and Silva [9]
by proving the existence of a second nontrivial solution under a non-quadradicity
condition at infinity on the non-linearity. Assuming more regularity on the
non-linearity f, we are able to prove the existence of at least three nontrivial
solutions.
Submitted February 28, 2020. Published June 16, 2020.
Math Subject Classifications: 35J20.
Key Words: Semilinear elliptic boundary value problem;
superlinear subcritical growth; infinite dimensional Morse theory;
critical groups.
Show me the PDF file (361 KB),
TEX file for this article.
 |
Leandro L. Recôva
T-Mobile Inc.
Ontario, CA 91761, USA
email: leandro.recova3@t-mobile.com
|
|---|
 |
Adolfo J. Rumbos
Department of Mathematics
Pomona College
Claremont, CA 91711, USA
email: arumbos@pomona.edu
|
|---|
Return to the EJDE web page
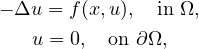
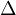 denotes the N-dimensional Laplacian,
denotes the N-dimensional Laplacian,
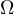 is a bounded domain
with smooth boundary,
is a bounded domain
with smooth boundary,
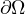 , in
, in
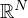
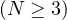 , and
f is a continuous function having subcritical growth in the second variable.
Using infinite-dimensional Morse theory, we extended the results of Furtado
and Silva [9]
by proving the existence of a second nontrivial solution under a non-quadradicity
condition at infinity on the non-linearity. Assuming more regularity on the
non-linearity f, we are able to prove the existence of at least three nontrivial
solutions.
, and
f is a continuous function having subcritical growth in the second variable.
Using infinite-dimensional Morse theory, we extended the results of Furtado
and Silva [9]
by proving the existence of a second nontrivial solution under a non-quadradicity
condition at infinity on the non-linearity. Assuming more regularity on the
non-linearity f, we are able to prove the existence of at least three nontrivial
solutions.

