Electron. J. Differential Equations, Vol. 2020 (2020), No. 72, pp. 1-20
Representation of solutions of a second order delay differential equation
Kee Qiu, Jinrong Wang
Abstract:
In this article, we study an inhomogeneous second order delay differential equation
on the fractal set
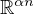
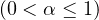 ,
based on the theory of
local calculus. We introduce delay cosine and sine type matrix functions
and give their properties on the fractal set. We give the representation of solutions
to second order differential equations with pure delay and two delays.
,
based on the theory of
local calculus. We introduce delay cosine and sine type matrix functions
and give their properties on the fractal set. We give the representation of solutions
to second order differential equations with pure delay and two delays.
Submitted March 24, 2020. Published July 7, 2020.
Math Subject Classifications: 26A33, 28A80, 34A34.
Key Words: Second order delay differential equations; delayed matrix functions;
fractal set.
DOI: 10.58997/ejde.2020.72
Show me the PDF file (355 KB),
TEX file for this article.
 |
Kee Qiu
School of Mathematics and Big Data
Guizhou Education University
Guiyang, Guizhou 550018, China
email: qke456@sina.com
|
|---|
 |
Jinrong Wang
Department of Mathematics
Guizhou University
Guiyang, Guizhou 550025, China
email: jrwang@gzu.edu.cn
|
|---|
Return to the EJDE web page
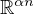
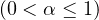 ,
based on the theory of
local calculus. We introduce delay cosine and sine type matrix functions
and give their properties on the fractal set. We give the representation of solutions
to second order differential equations with pure delay and two delays.
,
based on the theory of
local calculus. We introduce delay cosine and sine type matrix functions
and give their properties on the fractal set. We give the representation of solutions
to second order differential equations with pure delay and two delays.

