Electron. J. Differential Equations, Vol. 2020 (2020), No. 87, pp. 1-14.
Oscillatory behavior for nonlinear homogeneous neutral difference equations of
second order with coefficient changing sign
Ajit Kumar Bhuyan, Laxmi Narayan Padhy, Radhanath Rath
Abstract:
In this article, we obtain sufficient conditions so that all solutions of the neutral
difference equation
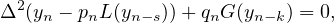
and all unbounded solutions of the neutral difference equation
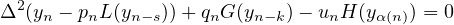
are oscillatory,
where
 ,
,
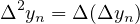 .
Different types of super linear and sub linear conditions are imposed on
G to prevent the solution approaching zero or
.
Different types of super linear and sub linear conditions are imposed on
G to prevent the solution approaching zero or
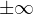 .
.
Submitted June 3, 2020. Published August 12, 2020.
Math Subject Classifications: 39A10, 39A12.
Key Words: Oscillatory solution; nonoscillatory solution; asymptotic behavior;
difference equation.
DOI: 10.58997/ejde.2020.87
Show me the PDF file (368 KB),
TEX file for this article.
 |
Ajit Kumar Bhuyan
Dept. Of Mathematics
Sai international School
Bhubaneswar, Odisha, India
email: ajitbhuyan13@gmail.com
|
|---|
 |
Laxmi Narayan Padhy
Dept. of Math and Computer Science
Konark Institute of Science and Technology
Bhubaneswar, Odisha, India
email: padhyln@gmail.com
|
|---|
 |
Radhanath Rath
VSSUT Burla, 768018
Retired Principalhallikote Autonomous College
Berhampur, Odisha, India
email: radhanathmath@yahoo.co.in
|
|---|
Return to the EJDE web page
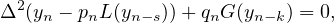
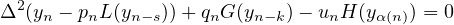
 ,
,
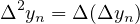 .
Different types of super linear and sub linear conditions are imposed on
G to prevent the solution approaching zero or
.
Different types of super linear and sub linear conditions are imposed on
G to prevent the solution approaching zero or
 .
.


