In this work we consider the class of nonlocal non-autonomous evolution problems in a bounded smooth domain
 in
in


with u(t,x)= 0 for
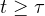 and
and
 .
Under appropriate assumptions we study the asymptotic behavior
of the evolution process, generated by this problem in a suitable Banach space.
We prove results on existence, uniqueness and smoothness of the solutions and on the
existence of pullback attractor for the evolution process.
We also prove a continuous dependence of the evolution process with respect to the
external stimuli function present in the model.
Furthermore, using the continuous dependence of the evolution process,
we prove the upper semicontinuity of pullback attractors with respect to the
external stimuli function. We finish this article with a small discussion about
the model and about a biological interpretation of the result on the continuous
dependence of neuronal activity with respect to the external stimuli function.
.
Under appropriate assumptions we study the asymptotic behavior
of the evolution process, generated by this problem in a suitable Banach space.
We prove results on existence, uniqueness and smoothness of the solutions and on the
existence of pullback attractor for the evolution process.
We also prove a continuous dependence of the evolution process with respect to the
external stimuli function present in the model.
Furthermore, using the continuous dependence of the evolution process,
we prove the upper semicontinuity of pullback attractors with respect to the
external stimuli function. We finish this article with a small discussion about
the model and about a biological interpretation of the result on the continuous
dependence of neuronal activity with respect to the external stimuli function.
