Electron. J. Differential Equations,
Vol. 2021 (2021), No. 14, pp. 1-31.
Existence and concentration results for fractional Schrodinger-Poisson system
via penalization method
Zhipeng Yang, Wei Zhang, Fukun Zhao
Abstract:
This article concerns the positive solutions for the fractional Schrodinger-Poisson system

where
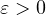 is a small parameter,
is a small parameter,
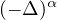 denotes the fractional
Laplacian of orders
denotes the fractional
Laplacian of orders
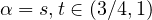 ,
,
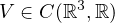 is
the potential function and
is
the potential function and
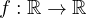 is continuous and
subcritical. Under a local condition imposed on the potential function, we relate the
number of positive solutions with the topology of the set where the potential attains
its minimum values. Moreover, we considered some properties of these positive solutions,
such as concentration behavior and decay estimate. In the proofs we apply variational methods,
penalization techniques and Ljusternik-Schnirelmann theory.
is continuous and
subcritical. Under a local condition imposed on the potential function, we relate the
number of positive solutions with the topology of the set where the potential attains
its minimum values. Moreover, we considered some properties of these positive solutions,
such as concentration behavior and decay estimate. In the proofs we apply variational methods,
penalization techniques and Ljusternik-Schnirelmann theory.
Submitted October 5, 2018. Published March 16, 2021.
Math Subject Classifications: 49J35, 58E05.
Key Words: Penalization method; fractional Schrodinger-Poisson;
Lusternik-Schnirelmann theory.
DOI: https://doi.org/10.58997/ejde.2021.14
Show me the PDF file (450 KB),
TEX file for this article.
 |
Zhipeng Yang
Department of Mathematics
Yunnan Normal University
Kunming 650500, China
email: yangzhipeng326@163.com
|
|---|
 |
Wei Zhang
School of Statistics and Mathematics
Yunnan University of Finance and Economics
Kunming 650221, China
email: weizyn@163.com
|
|---|
 |
Fukun Zhao
Department of Mathematics
Yunnan Normal University
Kunming 650500, China
email: fukunzhao@163.com
|
|---|
Return to the EJDE web page

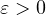 is a small parameter,
is a small parameter,
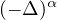 denotes the fractional
Laplacian of orders
denotes the fractional
Laplacian of orders
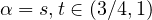 ,
,
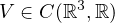 is
the potential function and
is
the potential function and
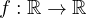 is continuous and
subcritical. Under a local condition imposed on the potential function, we relate the
number of positive solutions with the topology of the set where the potential attains
its minimum values. Moreover, we considered some properties of these positive solutions,
such as concentration behavior and decay estimate. In the proofs we apply variational methods,
penalization techniques and Ljusternik-Schnirelmann theory.
is continuous and
subcritical. Under a local condition imposed on the potential function, we relate the
number of positive solutions with the topology of the set where the potential attains
its minimum values. Moreover, we considered some properties of these positive solutions,
such as concentration behavior and decay estimate. In the proofs we apply variational methods,
penalization techniques and Ljusternik-Schnirelmann theory.


