Electron. J. Differential Equations, Vol. 2021 (2021), No. 48, pp. 1-12.
Multiple solutions to boundary value problems for semilinear elliptic equations
Duong Trong Luyen, Nguyen Minh Tri
Abstract:
In this article, we study the multiplicity of weak
solutions to the boundary value problem
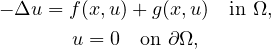
where Ω is a bounded domain with smooth boundary in RN (N > 2),
f(x,ξ) is odd in ξ and g is a perturbation term.
Under some growth conditions on f and g, we show that there are infinitely many
solutions. Here we do not require that f be continuous or satisfy the
Ambrosetti-Rabinowitz (AR) condition.
The conditions assumed here are not implied by the ones in [3,15].
We use the perturbation method by Rabinowitz combined with estimating the
asymptotic behavior of eigenvalues for Schrödinger's equations.
Submitted September 18, 2019. Published May 28, 2021.
Math Subject Classifications: 35J60, 35B33, 35J25, 35J70.
Key Words: Semilinear elliptic equations; multiple solutions; critical points;
perturbation methods; boundary value problem.
DOI: https://doi.org/10.58997/ejde.2021.48
Show me the PDF file (341 KB),
TEX file for this article.
 |
Duong Trong Luyen
Division of Computational Mathematics and Engineering
Institute for Computational Science, and
Faculty of Mathematics and Statistics
Ton Duc Thang University, Ho Chi Minh City, Vietnam
email: duongtrongluyen@tdtu.edu.vn
|
|---|
| |
Nguyen Minh Tri
Institute of Mathematics
Vietnam Academy of Science and Technology
18 Hoang Quoc Viet
10307 Cau Giay, Hanoi, Vietnam
email: triminh@math.ac.vn
|
|---|
Return to the EJDE web page