Farid Bozorgnia, Peter Lewintan
Abstract:
In this note, we study the asymptotic behavior, as t tends to infinity,
of the solution u to the evolutionary damped p-Laplace equation
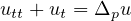
with Dirichlet boundary conditions. Let u* denote the stationary solution with
same boundary values, then we prove the W1,p-norm of u(t) - u* decays
for large t like t-1/((p-1)p), in the degenerate case p>2.
Submitted July 8, 2021. Published September 10, 2021.
Math Subject Classifications: 35B40, 35L70.
Key Words: p-Laplace; telegraph equation; asymptotic behavior; convexity.
DOI: https://doi.org/10.58997/ejde.2021.73
Show me the PDF file (334 KB), TEX file for this article.
 |
Farid Bozorgnia CAMGSD, Instituto Superior Técnico University of Lisbon Av. Rovisco Pais 1049-001 Lisbon, Portugal email: farid.bozorgnia@tecnico.ulisboa.pt |
|---|---|
 |
Peter Lewintan Faculty of Mathematics University of Duisburg-Essen Thea-Leymann-Str. 9, 45127 Essen, Germany email: peter.lewintan@uni-due.de |
Return to the EJDE web page