Electron. J. Differential Equations, Vol. 2022 (2022), No. 25, pp. 1-29.
Fractional Kirchhoff Hardy problems with weighted Choquard and singular nonlinearity
Sarika Goyal, Tarun Sharma
Abstract:
In this article, we study the existence and multiplicity of solutions to the
fractional Kirchhoff Hardy problem involving weighted Choquard and singular nonlinearity

where
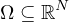 is an open bounded domain with smooth boundary
containing 0 in its interior,
is an open bounded domain with smooth boundary
containing 0 in its interior,
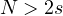 with
with
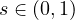 ,
,
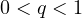 ,
,
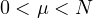 ,
,
 and
and
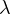 are positive parameters,
are positive parameters,
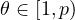 with
with
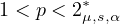 , where
, where
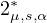 is the upper critical exponent
in the sense of weighted Hardy-Littlewood-Sobolev inequality.
Moreover
is the upper critical exponent
in the sense of weighted Hardy-Littlewood-Sobolev inequality.
Moreover
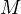 models a Kirchhoff coefficient, l is a positive weight and r is a
sign-changing function. Under the suitable assumption on l and r, we established
the existence of two positive solutions to the above problem by Nehari-manifold and
fibering map analysis with respect to the parameters.The results obtained
here are new even for s=1.
models a Kirchhoff coefficient, l is a positive weight and r is a
sign-changing function. Under the suitable assumption on l and r, we established
the existence of two positive solutions to the above problem by Nehari-manifold and
fibering map analysis with respect to the parameters.The results obtained
here are new even for s=1.
Submitted December 30, 2021. Published March 25, 2022.
Math Subject Classifications: 35A15, 35J75, 36B38.
Key Words: Fractional Kirchhoff Hardy operator; singular nonlinearity;
\hfill\break\indent weighted Choquard type nonlinearity;
Nehari-manifold; fibering map.
DOI: https://doi.org/10.58997/ejde.2022.25
Show me the PDF file (461 KB),
TEX file for this article.
 |
|---|
 |
Sarika Goyal
Department of Mathematics
Bennett University
Greater Noida, Uttar Pradesh, India
email: sarika1.iitd@gmail.com
|
|---|
Tarun Sharma
Department of Mathematics
Bennett University
Greater Noida, Uttar Pradesh, India
email: tarunsharma80065@gmail.com
|
Return to the EJDE web page

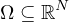 is an open bounded domain with smooth boundary
containing 0 in its interior,
is an open bounded domain with smooth boundary
containing 0 in its interior,
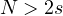 with
with
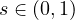 ,
,
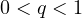 ,
,
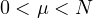 ,
,
 and
and
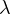 are positive parameters,
are positive parameters,
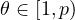 with
with
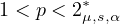 , where
, where
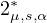 is the upper critical exponent
in the sense of weighted Hardy-Littlewood-Sobolev inequality.
Moreover
is the upper critical exponent
in the sense of weighted Hardy-Littlewood-Sobolev inequality.
Moreover
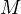 models a Kirchhoff coefficient, l is a positive weight and r is a
sign-changing function. Under the suitable assumption on l and r, we established
the existence of two positive solutions to the above problem by Nehari-manifold and
fibering map analysis with respect to the parameters.The results obtained
here are new even for s=1.
models a Kirchhoff coefficient, l is a positive weight and r is a
sign-changing function. Under the suitable assumption on l and r, we established
the existence of two positive solutions to the above problem by Nehari-manifold and
fibering map analysis with respect to the parameters.The results obtained
here are new even for s=1.

