Electron. J. Differential Equations, Vol. 2022 (2022), No. 27, pp. 1-15.
Second order Sobolev regularity for p-harmonic functions in SU(3)
Chengwei Yu
Abstract:
Let u be a weak solution to the degenerate subelliptic p-Laplacian equation
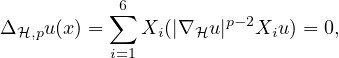
where
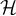 is the orthogonal complement of a Cartan subalgebra in SU(3) and its
orthonormal basis is composed of the vector fields X1,...,X6.
We prove that when 1<p<7/2, the solution u has the second order horizontal Sobolev
is the orthogonal complement of a Cartan subalgebra in SU(3) and its
orthonormal basis is composed of the vector fields X1,...,X6.
We prove that when 1<p<7/2, the solution u has the second order horizontal Sobolev
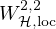 -regularity.
-regularity.
Submitted December 2, 2021. Published April 6, 2022.
Math Subject Classifications: 35H20, 35B65.
Key Words: p-Laplacian equation; SU(3);
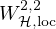 -regularity; Hessian matrix; p-harmonic function.
-regularity; Hessian matrix; p-harmonic function.
DOI: https://doi.org/10.58997/ejde.2022.27
Show me the PDF file (366 KB),
TEX file for this article.
 |
Chengwei Yu
School of Mathematical Sciences
Beihang University
Haidian District, Beijing 100191, China
email: chengweiyu@buaa.edu.cn
|
|---|
Return to the EJDE web page
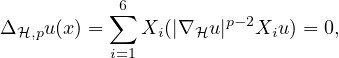
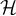 is the orthogonal complement of a Cartan subalgebra in SU(3) and its
orthonormal basis is composed of the vector fields X1,...,X6.
We prove that when 1<p<7/2, the solution u has the second order horizontal Sobolev
is the orthogonal complement of a Cartan subalgebra in SU(3) and its
orthonormal basis is composed of the vector fields X1,...,X6.
We prove that when 1<p<7/2, the solution u has the second order horizontal Sobolev
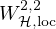 -regularity.
-regularity.
