Electron. J. Differential Equations, Vol. 2022 (2022), No. 36, pp. 1-18.
Weak solution by the sub-supersolution method for a nonlocal system
involving Lebesgue generalized spaces
Abdolrahman Razani, Giovany M. Figueiredo
Abstract:
We consider a system of nonlocal elliptic equations
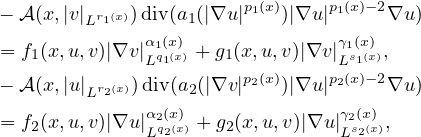
with Dirichlet boundary condition, where
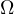 is a bounded domain in
is a bounded domain in
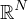
 with
with
 boundary. Using sub-supersolution method,
we prove the existence of at least one positive weak solution.
Also, we study a generalized logistic equation and a sublinear system.
boundary. Using sub-supersolution method,
we prove the existence of at least one positive weak solution.
Also, we study a generalized logistic equation and a sublinear system.
Submitted June 18, 2021. Published May 1, 2022
Math Subject Classifications: 35J91, 35J60, 35D30.
Key Words: Nonlocal problem, p(x)-Laplacian, sub-supersolution; minimal wave speed.
DOI: https://doi.org/10.58997/ejde.2022.36
Show me the PDF file (406 KB),
TEX file for this article.
 |
Abdolrahman Razani
Department of Pure Mathematics
Faculty of Science
Imam Khomeini International University
Postal code: 34148-96818, Qazvin, Iran
email: razani@sci.ikiu.ac.ir
|
|---|
 |
Giovany M. Figueiredo
Departamento de Matemática
Universidade de Brasilia
70.910-900, Brasilia (DF), Brazil
email: giovany@unb.br
|
|---|
Return to the EJDE web page
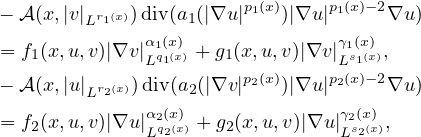
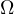 is a bounded domain in
is a bounded domain in
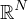
 with
with
 boundary. Using sub-supersolution method,
we prove the existence of at least one positive weak solution.
Also, we study a generalized logistic equation and a sublinear system.
boundary. Using sub-supersolution method,
we prove the existence of at least one positive weak solution.
Also, we study a generalized logistic equation and a sublinear system.

