Electron. J. Differential Equations, Vol. 2022 (2022), No. 62, pp. 1-28.
Higher differentiability for solutions to nonhomogeneous obstacle problems
with 1<p<2
Zhenqiang Wang
Abstract:
In this article, we establish integer and fractional higher-order
differentiability of weak solutions to non-homogeneous obstacle problems
that satisfy the variational inequality
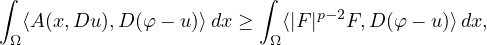
where 1<p<2,
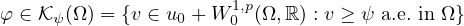 ,
,
 is a fixed boundary datum.
We show that the higher differentiability of integer or fractional order of the
gradient of the obstacle ψ and the nonhomogeneous term F can transfer to
the gradient of the weak solution, provided the partial map
is a fixed boundary datum.
We show that the higher differentiability of integer or fractional order of the
gradient of the obstacle ψ and the nonhomogeneous term F can transfer to
the gradient of the weak solution, provided the partial map
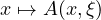 belongs to a suitable Sobolev or Besov-Lipschitz space.
belongs to a suitable Sobolev or Besov-Lipschitz space.
Submitted May 23, 2022. Published August 22, 2022.
Math Subject Classifications: 35J87, 49J40, 47J20.
Key Words: Nonhomogeneous elliptic obstacle problems; higher differentiability;
Sobolev coefficients; Besov-Lipschitz coefficients.
DOI: https://doi.org/10.58997/ejde.2022.62
Show me the PDF file (447 KB),
TEX file for this article.
 |
Zhenqiang Wang
School of Mathematical Sciences
Nankai University
Tianjin 300071, China
email: 2120190058@mail.nankai.edu.cn
|
|---|
Return to the EJDE web page
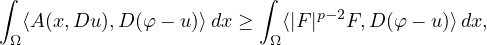
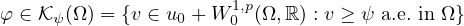 ,
,
 is a fixed boundary datum.
We show that the higher differentiability of integer or fractional order of the
gradient of the obstacle ψ and the nonhomogeneous term F can transfer to
the gradient of the weak solution, provided the partial map
is a fixed boundary datum.
We show that the higher differentiability of integer or fractional order of the
gradient of the obstacle ψ and the nonhomogeneous term F can transfer to
the gradient of the weak solution, provided the partial map
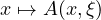 belongs to a suitable Sobolev or Besov-Lipschitz space.
belongs to a suitable Sobolev or Besov-Lipschitz space.
