Electron. J. Differential Equations, Vol. 2022 (2022), No. 85, pp. 1-21.
Monotonicity properties of the eigenvalues of nonlocal fractional operators and their applications
Giovanni Molica Bisci, Raffaella Servadei, Binlin Zhang
Abstract:
In this article we study an equation driven by the nonlocal integrodifferential
operator
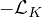 in presence of an asymmetric nonlinear term f.
Among the main results of the paper we prove the existence of at least a weak solution
for this problem, under suitable assumptions on the asymptotic behavior of the
nonlinearity f at
in presence of an asymmetric nonlinear term f.
Among the main results of the paper we prove the existence of at least a weak solution
for this problem, under suitable assumptions on the asymptotic behavior of the
nonlinearity f at
 . Moreover, we show the uniqueness of this solution,
under additional requirements on f.
We also give a non-existence result for the problem under consideration.
All these results were obtained using variational techniques and a monotonicity property
of the eigenvalues of
. Moreover, we show the uniqueness of this solution,
under additional requirements on f.
We also give a non-existence result for the problem under consideration.
All these results were obtained using variational techniques and a monotonicity property
of the eigenvalues of
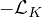 with respect to suitable weights, that we
prove along the present paper. This monotonicity property is of independent
interest and represents the nonlocal counterpart of a
famous result obtained by de Figueiredo and Gossez [14]
in the setting of uniformly elliptic operators.
with respect to suitable weights, that we
prove along the present paper. This monotonicity property is of independent
interest and represents the nonlocal counterpart of a
famous result obtained by de Figueiredo and Gossez [14]
in the setting of uniformly elliptic operators.
Submitted December 8, 2022. Published December 21, 2022.
Math Subject Classifications: 35A01, 35S15, 47G20, 45G05.
Key Words: Fractional Laplacian; integrodifferential operator; nonlocal problems;
eigenvalue and eigenfunction; asymmetric nonlinearities;
variational methods; critical point theory; saddle point theorem.
DOI: https://doi.org/10.58997/ejde.2022.85
Show me the PDF file (387 KB),
TEX file for this article.
 |
Giovanni Molica Bisci
Dipartimento di Scienze Pure e Applicate (DiSPeA)
Università degli Studi di Urbino Carlo Bo
Piazza della Repubblica 13, 61029 Urbino (Pesaro e Urbino), Italy
email: giovanni.molicabisci@uniurb.it
|
|---|
 |
Raffaella Servadei
Dipartimento di Scienze Pure e Applicate (DiSPeA)
Università degli Studi di Urbino Carlo Bo
Piazza della Repubblica 13, 61029 Urbino (Pesaro e Urbino), Italy
email: raffaella.servadei@uniurb.it
|
|---|
 |
Binlin Zhang
College of Mathematics and Systems Science
Shandong University of Science and Technology
Qingdao 266590, China
email: zhangbinlin2012@163.com
|
|---|
Return to the EJDE web page
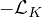 in presence of an asymmetric nonlinear term f.
Among the main results of the paper we prove the existence of at least a weak solution
for this problem, under suitable assumptions on the asymptotic behavior of the
nonlinearity f at
in presence of an asymmetric nonlinear term f.
Among the main results of the paper we prove the existence of at least a weak solution
for this problem, under suitable assumptions on the asymptotic behavior of the
nonlinearity f at
 . Moreover, we show the uniqueness of this solution,
under additional requirements on f.
We also give a non-existence result for the problem under consideration.
All these results were obtained using variational techniques and a monotonicity property
of the eigenvalues of
. Moreover, we show the uniqueness of this solution,
under additional requirements on f.
We also give a non-existence result for the problem under consideration.
All these results were obtained using variational techniques and a monotonicity property
of the eigenvalues of
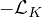 with respect to suitable weights, that we
prove along the present paper. This monotonicity property is of independent
interest and represents the nonlocal counterpart of a
famous result obtained by de Figueiredo and Gossez [14]
in the setting of uniformly elliptic operators.
with respect to suitable weights, that we
prove along the present paper. This monotonicity property is of independent
interest and represents the nonlocal counterpart of a
famous result obtained by de Figueiredo and Gossez [14]
in the setting of uniformly elliptic operators.


