Differential Equations and Computational Simulations III
Electron. J. Diff. Eqns., Conf. 01, 1997, pp. 109-117.
A bifurcation result for Sturm-Liouville problems with a set-valued term
Georg Hetzer
Abstract:
It is established in this note that
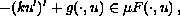
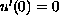 ,
,
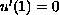
has a multiple bifurcation point at
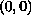 in the sense that infinitely many continua meet at
in the sense that infinitely many continua meet at
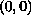 .
.
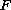 is a
``set-valued representation'' of a function with jump
discontinuities along the line segment
is a
``set-valued representation'' of a function with jump
discontinuities along the line segment
![$[0,1]\times\{0\}$](gifs/ag.gif) .
The proof relies on a Sturm-Liouville version of Rabinowitz's
bifurcation theorem and an approximation procedure.
.
The proof relies on a Sturm-Liouville version of Rabinowitz's
bifurcation theorem and an approximation procedure.
Published November 12, 1998.
Mathematics Subject Classification: 34B15, 34C23, 47H04, 86A10.
Key words and phrases: Differential inclusion, Sturm-Liouville problem,
Rabinowitz bifurcation.
Show me the
PDF file (115K),
TEX file, and other files for this article.
Georg Hetzer
Department of Mathematics,
Auburn University
Auburn, AL 36849-5310, USA
E-mail address: hetzege@mail.auburn.edu
Return to the Proceedings of Conferences:
Electr. J. Diff. Eqns.
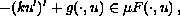
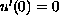 ,
,
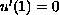
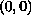 in the sense that infinitely many continua meet at
in the sense that infinitely many continua meet at
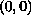 .
.
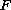 is a
``set-valued representation'' of a function with jump
discontinuities along the line segment
is a
``set-valued representation'' of a function with jump
discontinuities along the line segment
![$[0,1]\times\{0\}$](gifs/ag.gif) .
The proof relies on a Sturm-Liouville version of Rabinowitz's
bifurcation theorem and an approximation procedure.
.
The proof relies on a Sturm-Liouville version of Rabinowitz's
bifurcation theorem and an approximation procedure.