Differential Equations and Computational Simulations III
Electron. J. Diff. Eqns., Conf. 01, 1997, pp. 119, 127.
A global solution curve for a class of semilinear equations
Philip Korman
Abstract:
We use bifurcation theory to give a simple proof of existence and
uniqueness of a positive solution for the problem
 for
for
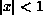 , u = 0 on |x| = 1,
, u = 0 on |x| = 1,
where
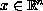 ,
for any positive integer n, and real
,
for any positive integer n, and real
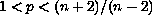 ,
,
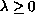 .
Moreover, we show that all solutions lie on a unique smooth curve of
solutions, and all solutions are non-singular. In the process we prove the
following assertion, which appears to be of independent interest: the Morse
index of the positive solution of
.
Moreover, we show that all solutions lie on a unique smooth curve of
solutions, and all solutions are non-singular. In the process we prove the
following assertion, which appears to be of independent interest: the Morse
index of the positive solution of
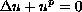 for
for 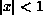 ,
u = 0 on |x| = 1
,
u = 0 on |x| = 1
is one, for any
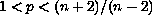 .
.
Published November 12, 1998.
Mathematics Subject Classifications: 35J60.
Key words and phrases: Uniqueness of positive solution, Morse index.
Show me the
PDF file (121K),
TEX file, and other files for this article.
Philip Korman
Institute for Dynamics and
Department of Mathematical Sciences
University of Cincinnati
Cincinnati Ohio 45221-0025 USA
E-mail address: kormanp@math.uc.edu
Return to the Proceedings of Conferences:
Electr. J. Diff. Eqns.
 for
for
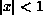 , u = 0 on |x| = 1,
, u = 0 on |x| = 1, 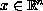 ,
for any positive integer n, and real
,
for any positive integer n, and real
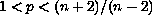 ,
,
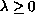 .
Moreover, we show that all solutions lie on a unique smooth curve of
solutions, and all solutions are non-singular. In the process we prove the
following assertion, which appears to be of independent interest: the Morse
index of the positive solution of
.
Moreover, we show that all solutions lie on a unique smooth curve of
solutions, and all solutions are non-singular. In the process we prove the
following assertion, which appears to be of independent interest: the Morse
index of the positive solution of
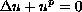 for
for 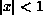 ,
u = 0 on |x| = 1
,
u = 0 on |x| = 1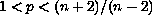 .
.