We study the existence of solutions to the fourth order semi-linear equation
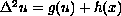 .
.
We show that there is a positive constant
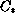 ,
such that if
,
such that if
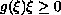 for
for
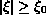 and
and
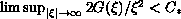 ,
then for all
,
then for all
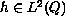 with
with
 ,
the above equation has a weak solution in
,
the above equation has a weak solution in
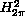 .
.
Chen Chang
Abstract:
We study the existence of solutions to the fourth order semi-linear equation
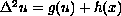 .
.
We show that there is a positive constant
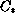 ,
such that if
,
such that if
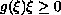 for
for
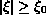 and
and
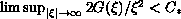 ,
then for all
,
then for all
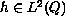 with
with
 ,
the above equation has a weak solution in
,
the above equation has a weak solution in
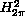 .
.
Published October 31, 2000.
Math Subject Classifications: 35J30, 35B10.
Key Words: periodic solutions, elliptic fourth-order PDE.
Show me the PDF file (136K), TEX file, and other files for this article.