16th Conference on Applied Mathematics, Univ. of Central Oklahoma,
Electron. J. Diff. Eqns., Conf. 07, 2001, pp. 71-88.
A two dimensional Hammerstein problem: The linear case
Jun Hua & James L. Moseley
Abstract:
Nonlinear equations of the form
![$L[u]=\lambda g(u)$](gifs/aa.gif) where
where
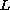 is a linear operator on a function space and
is a linear operator on a function space and
 maps
maps
 to the composition function
to the composition function
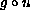 arise in the theory of spontaneous combustion. We assume
arise in the theory of spontaneous combustion. We assume
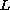 is invertible so that such an equation can be written as a Hammerstein
equation,
is invertible so that such an equation can be written as a Hammerstein
equation,
![$u=B[u]$](gifs/af.gif) where
where
![$B[u]=\lambda L^{-1}[g(u)]$](gifs/ag.gif) .
To investigate the importance of the growth rate of
.
To investigate the importance of the growth rate of
 and the sign and magnitude of
and the sign and magnitude of
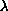 on the number of solutions of such problems, in a previous paper we
considered the one-dimensional problem
on the number of solutions of such problems, in a previous paper we
considered the one-dimensional problem
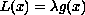 where
where
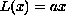 .
This paper extends these results to two dimensions for the linear case.
.
This paper extends these results to two dimensions for the linear case.
Published July 20, 2001.
Subject lassfications: 47H30.
Key words: Hammerstein problem, nonlinear differential equation.
Show me the
PDF file (254K),
TEX file, and other files for this article.
 |
Jun Hua
West Virginia University
Morgantown, West Virginia 26506-6310 USA |
|---|
 |
James L. Moseley
West Virginia University
Morgantown, West Virginia 26506-6310 USA
e-mail: moseley@math.wvu.edu
Telephone: 304-293-2011 |
|---|
Return to the EJDE web page
![$L[u]=\lambda g(u)$](gifs/aa.gif) where
where
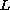 is a linear operator on a function space and
is a linear operator on a function space and
 maps
maps
 to the composition function
to the composition function
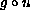 arise in the theory of spontaneous combustion. We assume
arise in the theory of spontaneous combustion. We assume
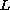 is invertible so that such an equation can be written as a Hammerstein
equation,
is invertible so that such an equation can be written as a Hammerstein
equation,
![$u=B[u]$](gifs/af.gif) where
where
![$B[u]=\lambda L^{-1}[g(u)]$](gifs/ag.gif) .
To investigate the importance of the growth rate of
.
To investigate the importance of the growth rate of
 and the sign and magnitude of
and the sign and magnitude of
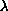 on the number of solutions of such problems, in a previous paper we
considered the one-dimensional problem
on the number of solutions of such problems, in a previous paper we
considered the one-dimensional problem
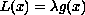 where
where
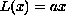 .
This paper extends these results to two dimensions for the linear case.
.
This paper extends these results to two dimensions for the linear case.

