We are interested in establishing properties of the general mathematical model
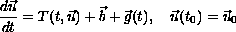
for the dynamical system defined by the (possibly nonlinear) operator
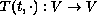 with state space
with state space
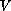 .
For one state variable where
.
For one state variable where
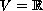 this may be written as
this may be written as
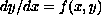 ,
,
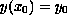 .
This paper establishes some mapping properties for the operator
.
This paper establishes some mapping properties for the operator
![$L[y]=dy/dx+p(x)y$](gifs/ag.gif) with
with
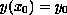 where
where
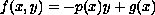 and
and
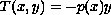 is linear. The conditions for the one-to-one property of the solution
map as a function of
is linear. The conditions for the one-to-one property of the solution
map as a function of
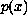 appear to be new or at least undocumented. This property is
needed in the development of a solution technique for a nonlinear model
for the agglomeration of point particles in a confined space (reactor).
appear to be new or at least undocumented. This property is
needed in the development of a solution technique for a nonlinear model
for the agglomeration of point particles in a confined space (reactor).
