2004-Fez conference on Differential Equations and Mechanics.
Electron. J. Diff. Eqns.,
Conference 11, 2004, pp. 11-21.
On the solvability of degenerated quasilinear elliptic problems
Youssef Akdim, Elhoussine Azroul, Mohamed Rhoudaf
Abstract:
In this article, we study the quasilinear elliptic problem
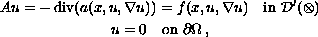
where
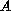 is a Leray-Lions operator from
is a Leray-Lions operator from
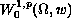 to
its dual
to
its dual
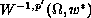 . We show that there exists a
solution
in
. We show that there exists a
solution
in
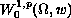 provided that
provided that
![$$
|f(x,r, \xi)|\leq \sigma^{1/q} [ g(x)+|r|^\eta \sigma^{\eta/q}
+ \sum_{i=1}^N w_i^{\delta/p}(x)|\xi_i|^\delta],
$$](gifs/af.gif)
where
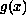 is a positive function in
is a positive function in
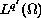 and
and
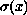 is
weight function and
is
weight function and
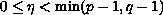 ,
,
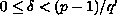 .
.
Published October 15, 2004.
Math Subject Classifications: 35J20, 35J25, 35J70.
Key Words: Weighted Sobolev spaces; variational calculus, Hardy inequality.
Show me the
PDF file (237K),
TEX file for this article.
 |
Youssef Akdim
Département de Mathématiques et Informatique,
Faculté des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fès, Maroc.
e-mail: akdimyoussef@yahoo.fr |
|---|
 |
Elhoussine Azroul
Département de Mathématiques et Informatique,
Faculté des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fès, Maroc.
e-mail: azroul_elhoussine@yahoo.fr |
|---|
 |
Mohamed Rhoudaf
Département de Mathématiques et Informatique,
Faculté des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fès, Maroc.
e-mail: rhoudaf_mohamed@yahoo.fr |
|---|
Return to the EJDE web page
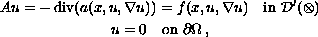
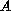 is a Leray-Lions operator from
is a Leray-Lions operator from
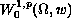 to
its dual
to
its dual
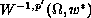 . We show that there exists a
solution
in
. We show that there exists a
solution
in
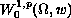 provided that
provided that
![$$
|f(x,r, \xi)|\leq \sigma^{1/q} [ g(x)+|r|^\eta \sigma^{\eta/q}
+ \sum_{i=1}^N w_i^{\delta/p}(x)|\xi_i|^\delta],
$$](gifs/af.gif)
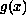 is a positive function in
is a positive function in
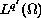 and
and
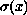 is
weight function and
is
weight function and
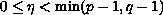 ,
,
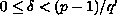 .
. 

