Seventh Mississippi State - UAB Conference on Differential Equations and Computational Simulations. Electron. J. Diff. Eqns., Conference 17 (2009), pp. 227-254.

Stationary radial solutions for a quasilinear Cahn-Hilliard model in N space dimensions

Peter Takac

Abstract:
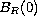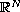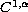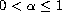We study the Neumann boundary value problem for stationary radial solutions of a quasilinear Cahn-Hilliard model in a ball $B_R(0)$ in $\mathbb{R}^N$. We establish new results on the existence, uniqueness, and multiplicity (by "branching") of such solutions. 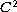We show striking differences in pattern formation produced by the Cahn-Hilliard model with the p-Laplacian and a $C^{1,\alpha}$ potential ($0<\alpha\leq 1$) in place of the regular (linear) Laplace operator and a $C^2$ potential. The corresponding energy functional exhibits one-dimensional continua ("curves") of critical points as opposed to the classical case with the Laplace operator. These facts offer a different explanation of the "slow dynamics" on the attractor for the dynamical system generated by the corresponding time-dependent parabolic problem.

Published April 15, 2009.
Math Subject Classifications: 35J20, 35B45, 35P30, 46E35.
Key Words: Generalized Cahn-Hilliard and bi-stable equations; radial p-Laplacian; phase plane analysis; first integral; nonuniqueness for initial value problems.

Show me the PDF file (482 KB), TEX file, and other files for this article.

Peter Takac
Institut für Mathematik, Universität Rostock
D-18055 Rostock, Germany
email: peter.takac@uni-rostock.de

Return to the table of contents for this conference.
Return to the EJDE web page